Python NumPy Cheat Sheet

This Python NumPy Cheat Sheet is a quick reference for NumPy beginners.

Given the fact that it’s one of the fundamental packages for scientific computing, NumPy is one of the packages that you must be able to use and know if you want to do data science with Python. It offers a great alternative to Python lists, as NumPy arrays are more compact, allow faster access in reading and writing items, and are more convenient and more efficient overall.

In addition, it’s (partly) the fundament of other important packages that are used for data manipulation and machine learning which you might already know, namely, Pandas, Scikit-Learn and SciPy:

• The Pandas data manipulation library builds on NumPy, but instead of the arrays, it makes use of two other fundamental data structures: Series and DataFrames,
• SciPy builds on Numpy to provide a large number of functions that operate on NumPy arrays, and
• The machine learning library Scikit-Learn builds not only on NumPy, but also on SciPy and Matplotlib.

You see, this Python library is a must-know: if you know how to work with it, you’ll also gain a better understanding of the other Python data science tools that you’ll undoubtedly be using.

It’s a win-win situation, right?

Nevertheless, just like any other library, NumPy can come off as quite overwhelming at start; What are the very basics that you need to know in order to get started with this data analysis library?

This cheat sheet means to give you a good overview of the possibilities that this library has to offer.

Go and check it out for yourself!

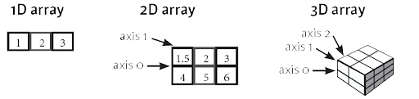
You’ll see that this cheat sheet covers the basics of NumPy that you need to get started: it provides a brief explanation of what the Python library has to offer and what the array data structure looks like, and goes on to summarize topics such as array creation, I/O, array examination, array mathematics, copying and sorting arrays, selection of array elements and shape manipulation.

NumPy arrays are often preferred over Python lists, and you’ll see that selecting elements from arrays is very similar to selecting elements from lists.

Do you want to know more? Check out myTechMint’s Python Tutorial.

NumPy

The NumPy library is the core library for scientific computing in Python. It provides a  high-performance multidimensional array object, and tools for working with these arrays.

Use the following improt convention:

import numpyas np

Numpy Arrays 

Creating Arrays

a = np.array([1,2,3])
b = np.array([(1.5,2,3), (4,5,6)], dtype = float)
c = np.array([[(1.5,2,3), (4,5,6)],[(3,2,1), (4,5,6)]], dtype = float)

Initial Placeholders

np.zeros((3,4)) #Create an array of zeros
np.ones((2,3,4),dtype=np.int16) #Create an array of ones
d = np.arange(10,25,5)#Create an array of evenly spaced values (step value)
np.linspace(0,2,9) #Create an array of evenlyspaced values (number of samples)
e = np.full((2,2),7)#Create a constant array
f = np.eye(2) #Create a 2X2 identity matrix
np.random.random((2,2)) #Create an array with random values
np.empty((3,2)) #Create an empty array

I/O

Saving & Loading on Disk

np.save('my_array' , a)
np.savez( 'array.npz', a, b)
np.load( 'my_array.npy')

Saving & Loading Text Files

np.loadtxt("myfile.txt")
np.genfromtxt("my_file.csv", delimiter= ',')
np.savetxt( "myarray.txt", a, delimiter= " ")

Asking For Help

np.info(np.ndarray.dtype)

Inspecting Your Array

a.shape #Array dimensions
len(a)#Length of array
b.ndim #Number of array dimensions
e.size #Number of array elements
b.dtype  #Data type of array elements
b.dtype.name  #Name of data type
b.astype(int). #Convert an array to a different type

Data Types

np.int64 #Signed 64-bit integer types
np.float32. #Standard double-precision floating point
np.complex. #Complex numbers represented by 128 floats
np.bool  #Boolean type storing TRUE and FALSE values
np.object #Python object type
np.string_ #Fixed-length string type
np.unicode_ #Fixed-length unicode type

Array Mathematics

Arithmetic Operations

g = a - b. #Subtraction
#array([[-0.5,0. ,0.], [-3. , -3. , -3. ]])
np.subtract(a,b) #Subtraction
b + a #Addition 
#array([[ 2.5, 4. , 6.],[5. ,7. ,9. ]])
np.add(b,a) #Addition 
a/b #Division 
#array([[0.66666667,1. ,1.],[0.25 ,0.4 ,0.5 ]])
np.divide(a,b) #Division 
a * b #Multiplication 
#array([[1.5, 4. ,9.],[ 4. , 10. , 18. ]])
np.multiply(a,b) #Multiplication 
np.exp(b) #Exponentiation
np.sqrt(b) #Square root
np.sin(a)  #Print sines of an array
np.cos(b) #Elementwise cosine
np.log(a)#Elementwise natural logarithm
e.dot(f) #Dot product 
#array([[7.,7.],[7.,7.]])

Comparison

a == b #Elementwise comparison array([[False , True, True], [ False,False ,False ]], dtype=bool) a< 2 #Elementwise comparison array([True, False, False], dtype=bool) np.array_equal(a, b) #Arraywise comparison

Copying Arrays

h = a.view()#Create a view of the array with the same data
np.copy(a) #Create a copy of the array
h = a.copy() #Create a deep copy of the array

Sorting Arrays

a.sort() #Sort an array
c.sort(axis=0) #Sort the elements of an array's axis

Subsetting, Slicing, Indexing

Subsetting

a[2] #Select the element at the 2nd index
#3
b[1,2] #Select the element at row 1 column 2(equivalent to b[1][2])
#6.0

Slicing

a[0:2]#Select items at index 0 and 1
#array([1, 2])
b[0:2,1] #Select items at rows 0 and 1 in column 1
#array([ 2.,5.])
b[:1] #Select all items at row0(equivalent to b[0:1, :])
#array([[1.5, 2., 3.]])
c[1,...] #Same as[1,:,:]
#array([[[ 3., 2.,1.],[ 4.,5., 6.]]])
a[ : : -1] #Reversed array a 
#array([3, 2, 1])

Boolean Indexing

a[a<2] #Select elements from a less than 2
#array([1])

Fancy Indexing

b[[1,0,1, 0],[0,1, 2, 0]] #Select elements(1,0),(0,1),(1,2) and(0,0)
#array([ 4. , 2. , 6. ,1.5])
b[[1,0,1, 0]][:,[0,1,2,0]] #Select a subset of the matrix’s rows and columns
#array([[ 4. ,5. , 6. , 4.],[1.5, 2. , 3. ,1.5],[ 4. ,5. , 6. , 4.],[1.5, 2. , 3. ,1.5]])

Array Manipulation

Transposing Array

i = np.transpose(b) #Permute array dimensions
i.T #Permute array dimensions

Changing Array Shape

b.ravel() #Flatten the array
g.reshape(3, -2) #Reshape, but don’t change data

Adding/Removing Elements

h.resize((2,6)) #Return a new arraywith shape(2,6)
np.append(h,g) #Append items to an array
np.insert(a,1,5)  #Insert items in an array
np.delete(a,[1])  #Delete items from an array

Combining Arrays

np.concatenate((a,d),axis=0) #Concatenate arrays
#array([1, 2, 3, 10, 15, 20])
np.vstack((a,b) #Stack arrays vertically(row wise)
#array([[1. , 2. , 3.],[1.5, 2. , 3.],[ 4. ,5. , 6. ]])
np.r_[e,f] #Stack arrays vertically(row wise)
np.hstack((e,f)) #Stack arrays horizontally(column wise)
#array([[7.,7.,1.,0.],[7.,7.,0.,1.]])
np.column_stack((a,d)) #Create stacked column wise arrays
#array([[1, 10],[ 2, 15],[ 3, 20]])
np.c_[a,d] #Create stacked column wise arrays

Splitting Arrays

np.hsplit(a,3) #Split the array horizontally at the 3rd index
#[array([1]),array([2]),array([3])]
np.vsplit(c,2) #Split the array vertically at the 2nd index
#[array([[[ 1.5, 2. ,1.],[ 4. ,5. , 6. ]]]),
#array([[[ 3., 2., 3.],[ 4.,5., 6.]]])]

Download Python NumPy Cheat Sheet