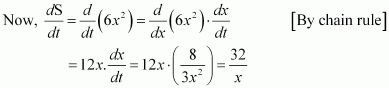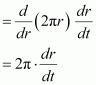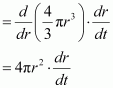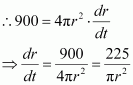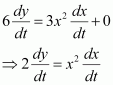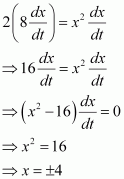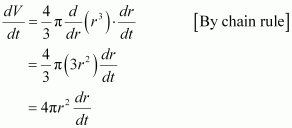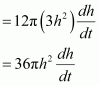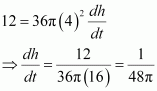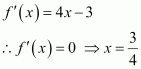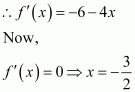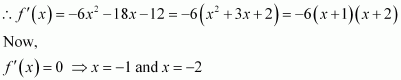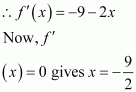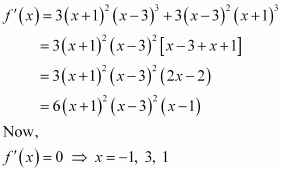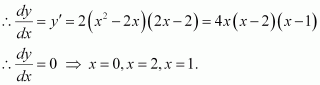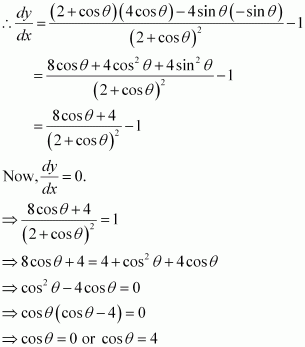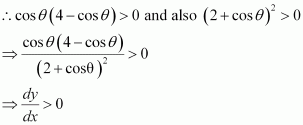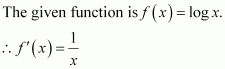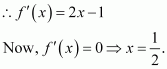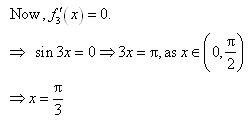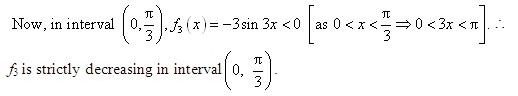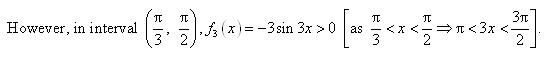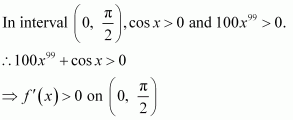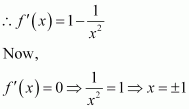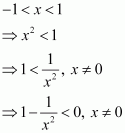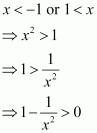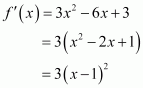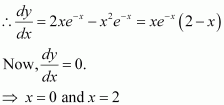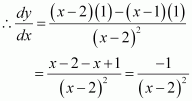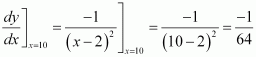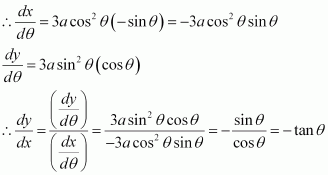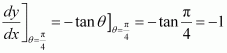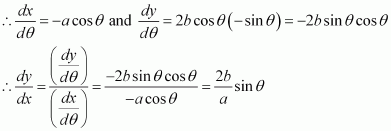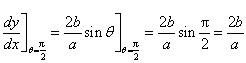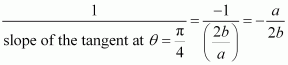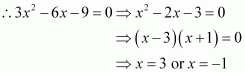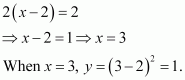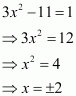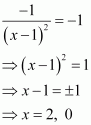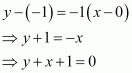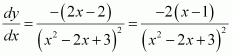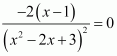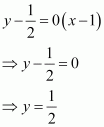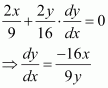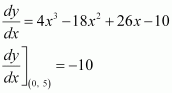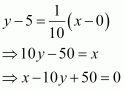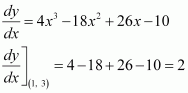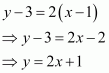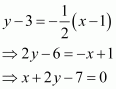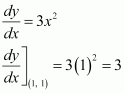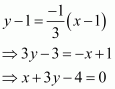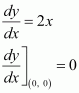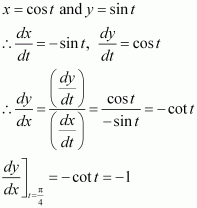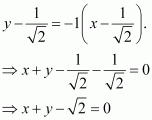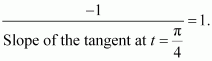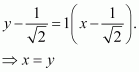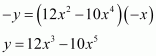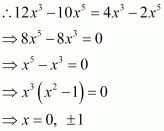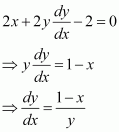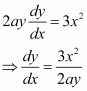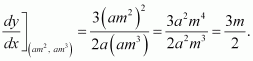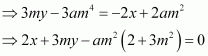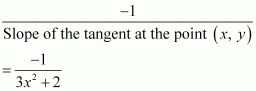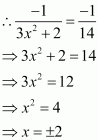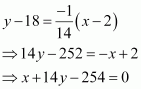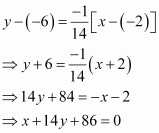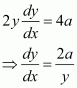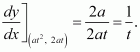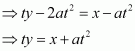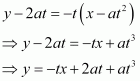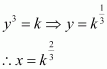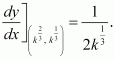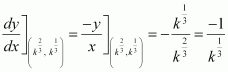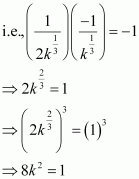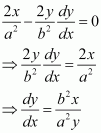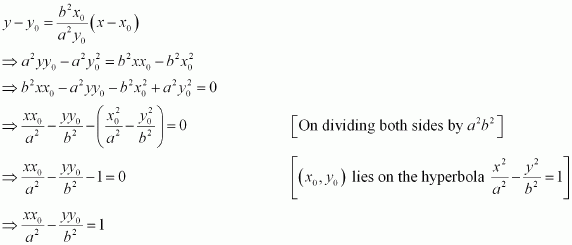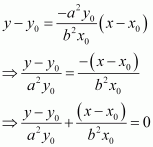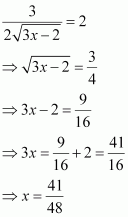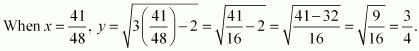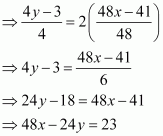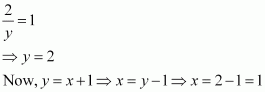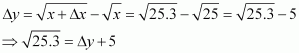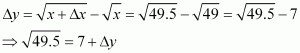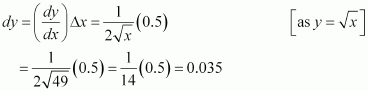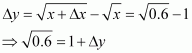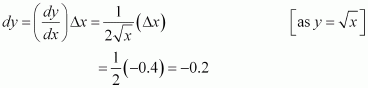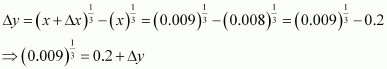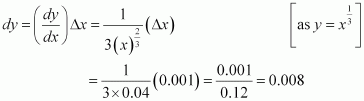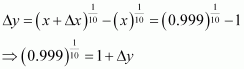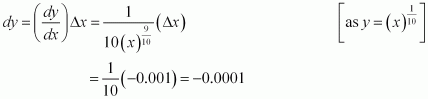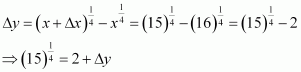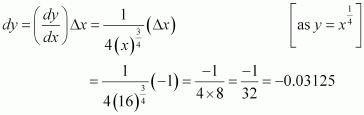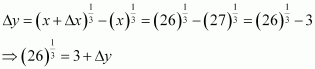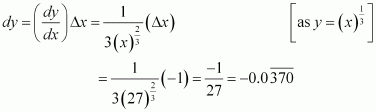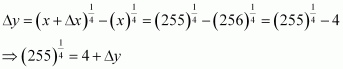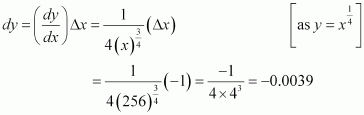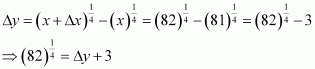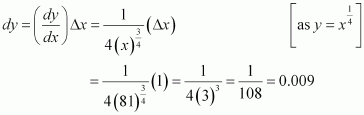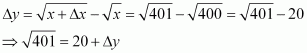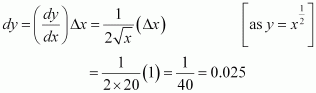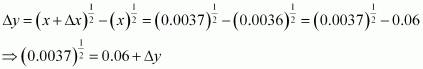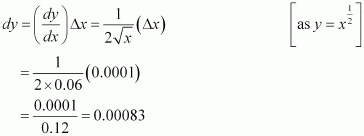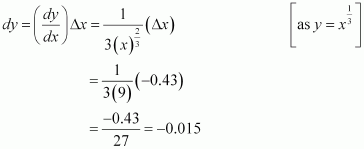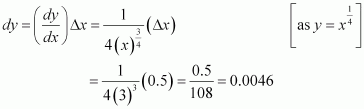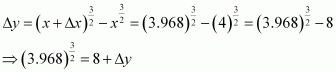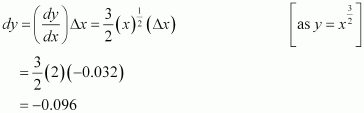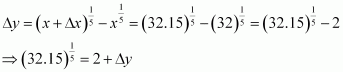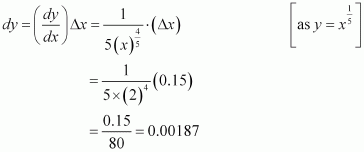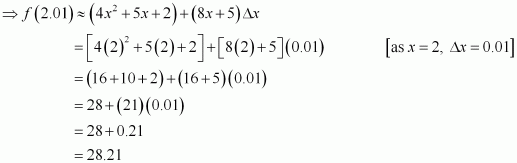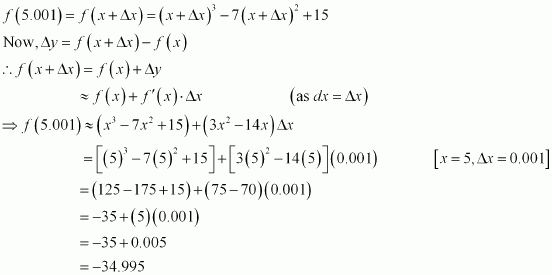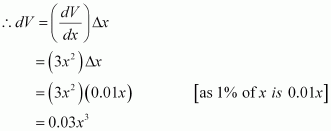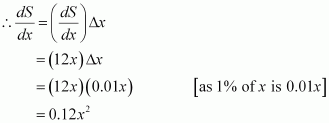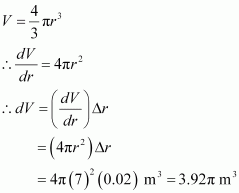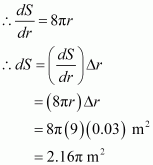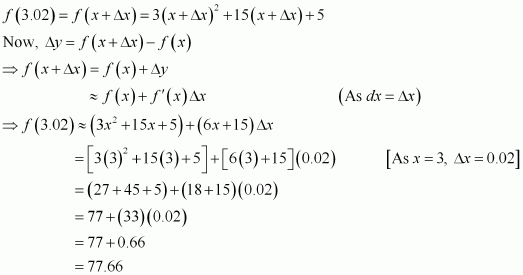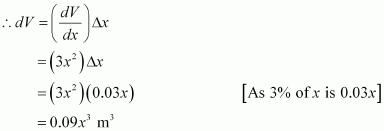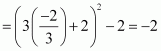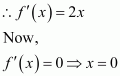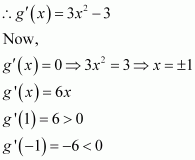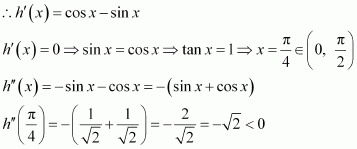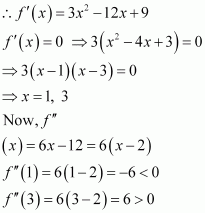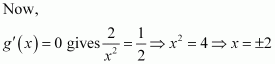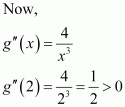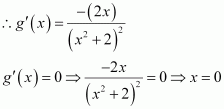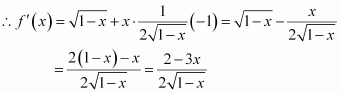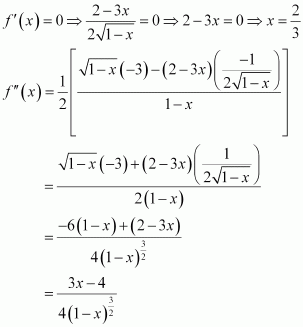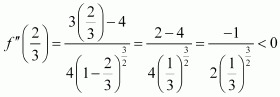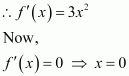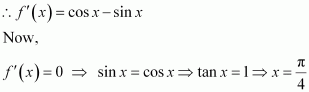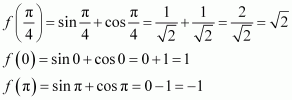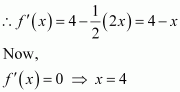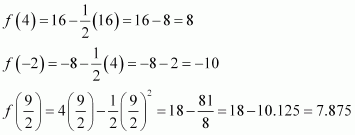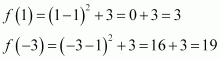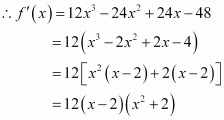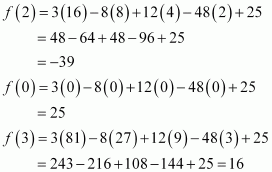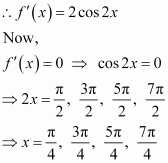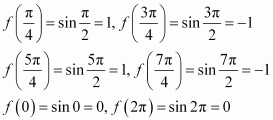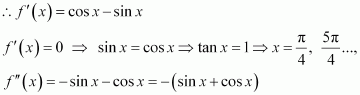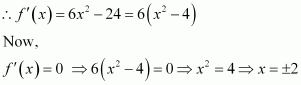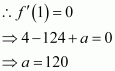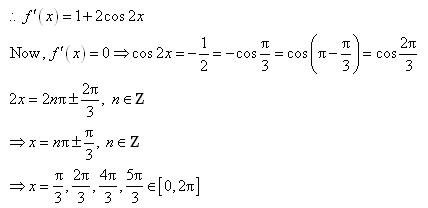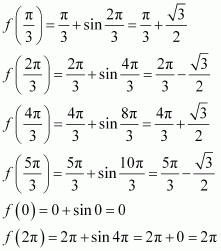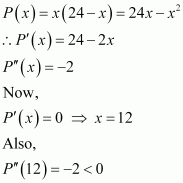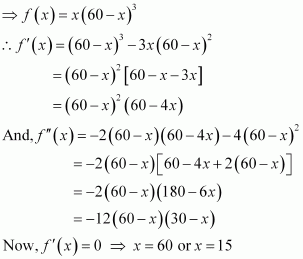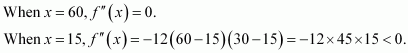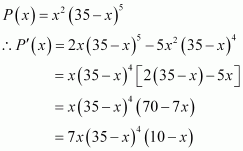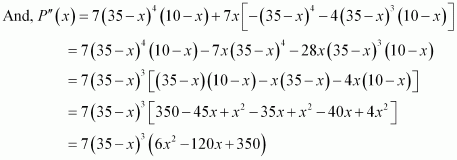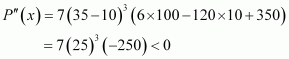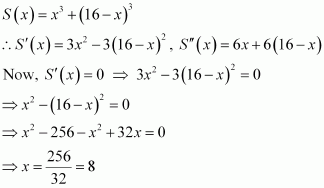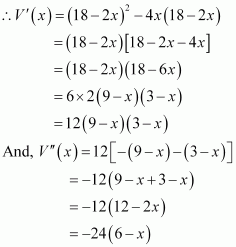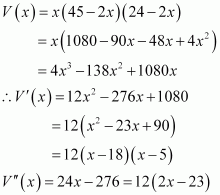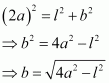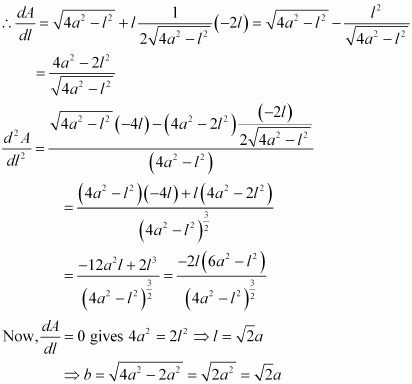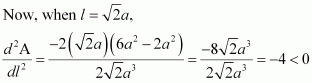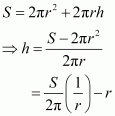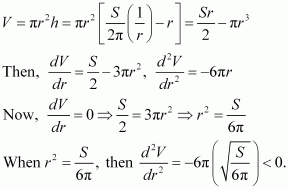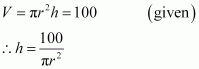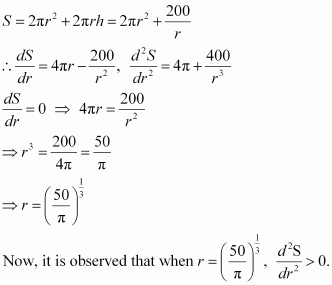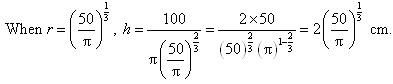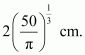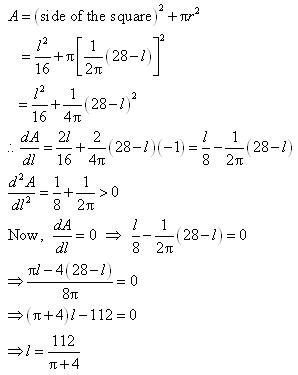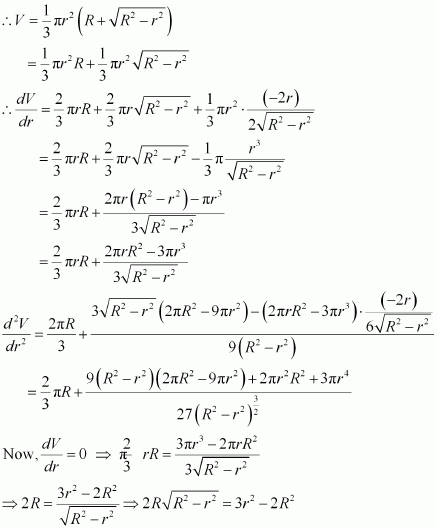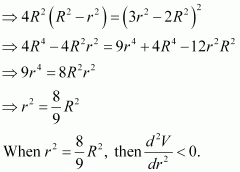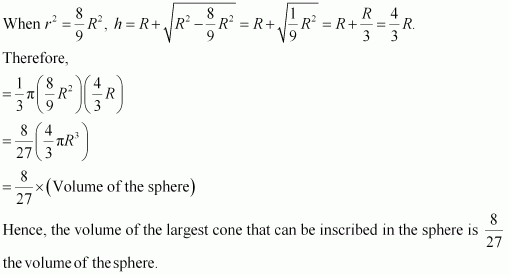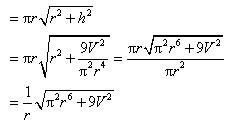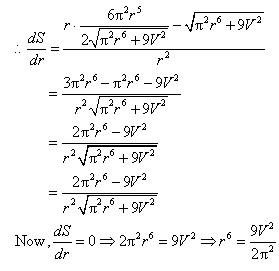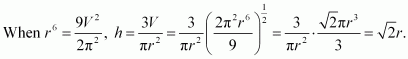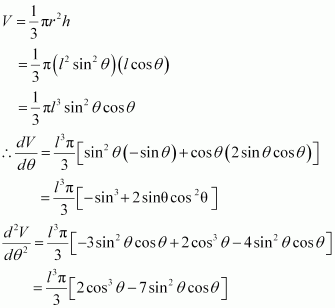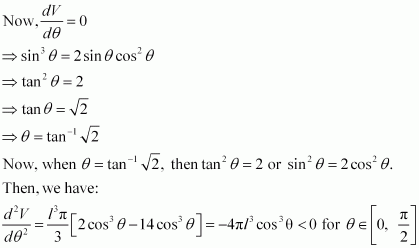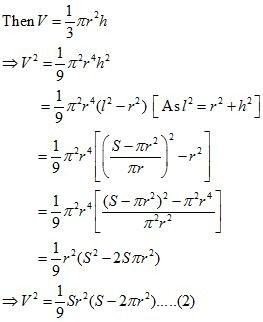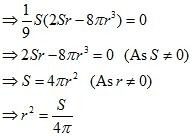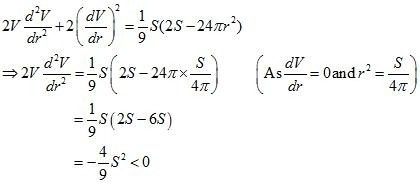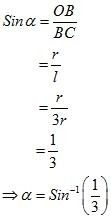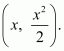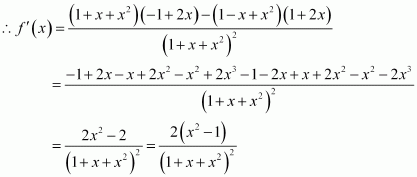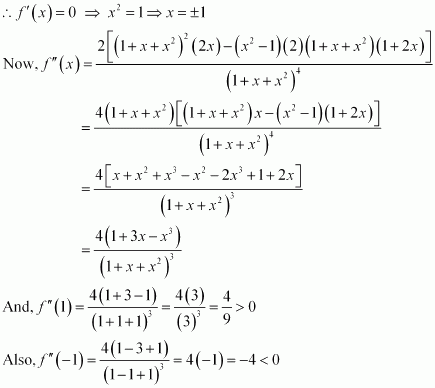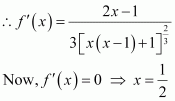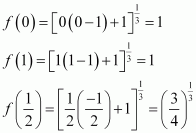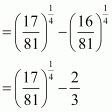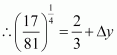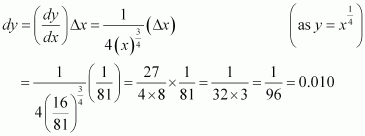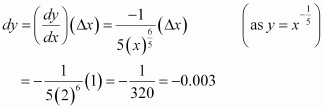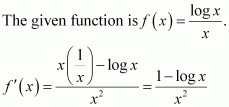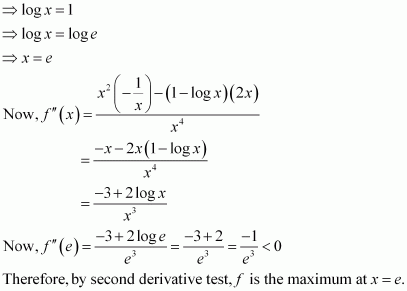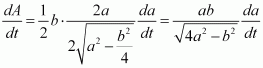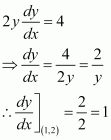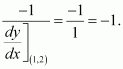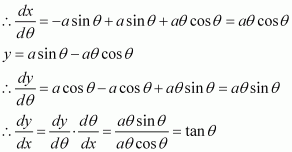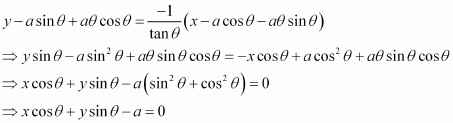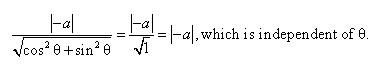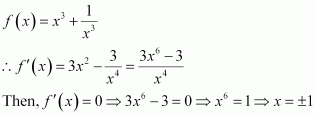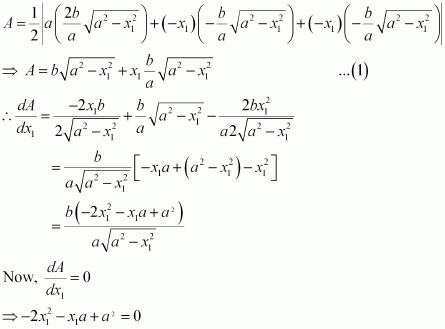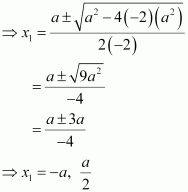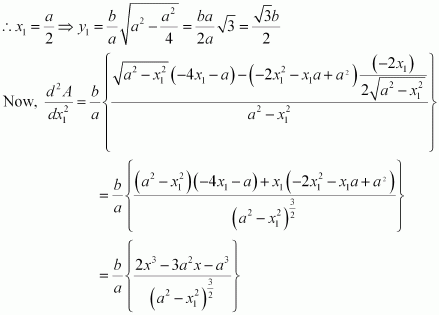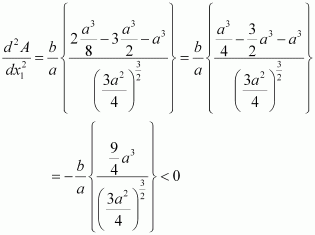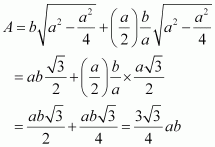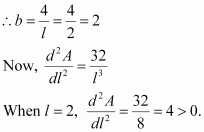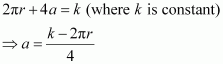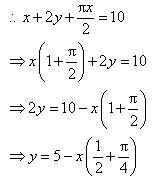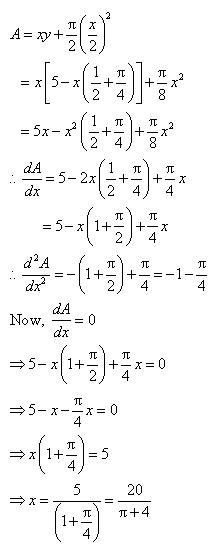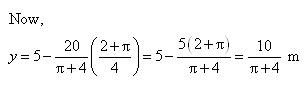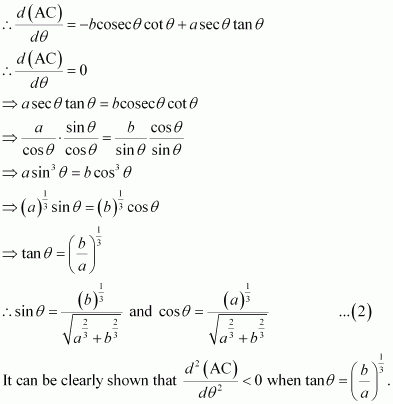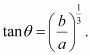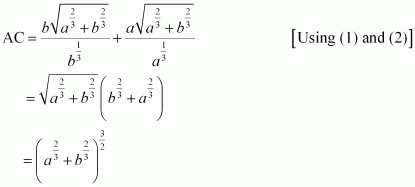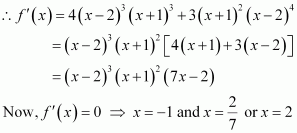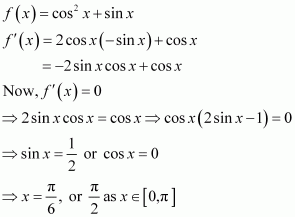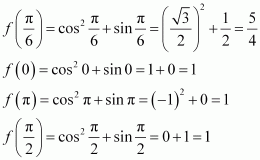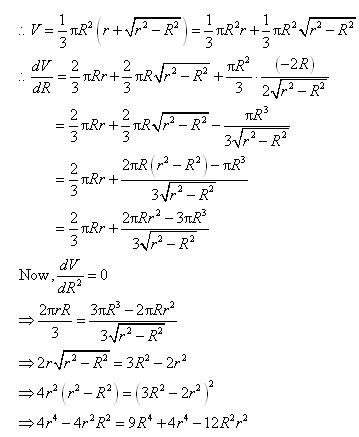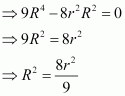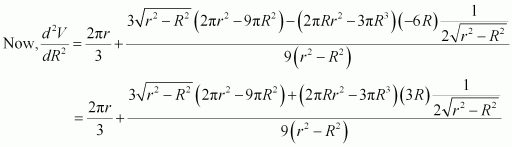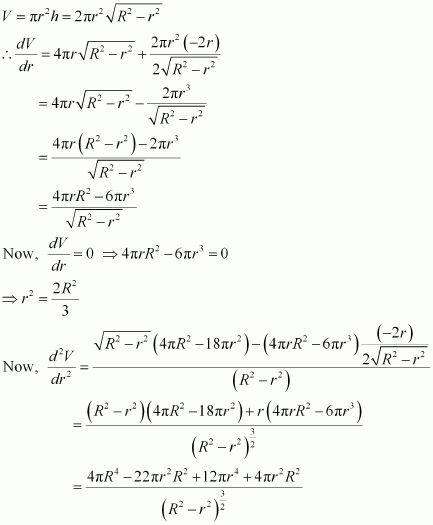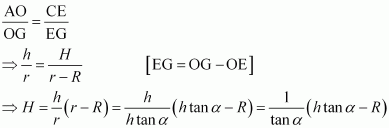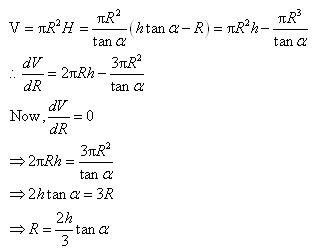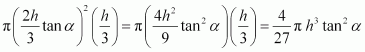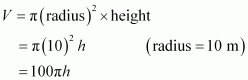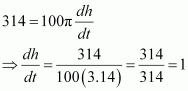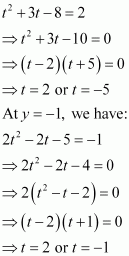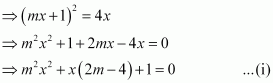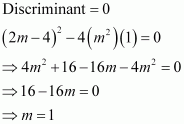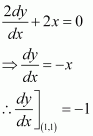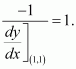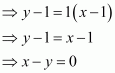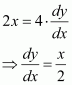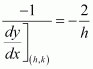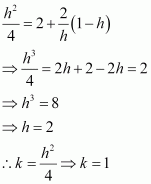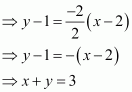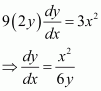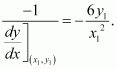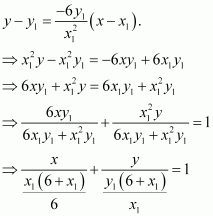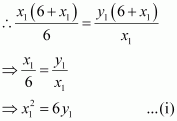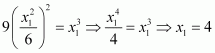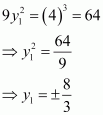Page No 197:
Question 1:
Find the rate of change of the area of a circle with respect to its radius r when
(a) r = 3 cm (b) r = 4 cm
Answer:
The area of a circle (A)with radius (r) is given by,
Now, the rate of change of the area with respect to its radius is given by,
- When r = 3 cm,
Hence, the area of the circle is changing at the rate of 6Ï€ cm when its radius is 3 cm.
- When r = 4 cm,
Hence, the area of the circle is changing at the rate of 8Ï€ cm when its radius is 4 cm.
Question 2:
The volume of a cube is increasing at the rate of 8 cm3/s. How fast is the surface area increasing when the length of an edge is 12 cm?
Answer:
Let x be the length of a side, V be the volume, and s be the surface area of the cube.
Then, V = x3 and S = 6x2 where x is a function of time t.
It is given that.
Then, by using the chain rule, we have:
∴
⇒
Thus, when x = 12 cm,
Hence, if the length of the edge of the cube is 12 cm, then the surface area is increasing at the rate of cm2/s.
Question 3:
The radius of a circle is increasing uniformly at the rate of 3 cm/s. Find the rate at which the area of the circle is increasing when the radius is 10 cm.
Answer:
The area of a circle (A) with radius (r) is given by,
Now, the rate of change of area (A) with respect to time (t) is given by,
It is given that,
∴
Thus, when r = 10 cm,
Hence, the rate at which the area of the circle is increasing when the radius is 10 cm is 60π cm2/s.
Question 4:
An edge of a variable cube is increasing at the rate of 3 cm/s. How fast is the volume of the cube increasing when the edge is 10 cm long?
Answer:
Let x be the length of a side and V be the volume of the cube. Then,
V = x3.
∴ (By chain rule)
It is given that,
∴
Thus, when x = 10 cm,
Hence, the volume of the cube is increasing at the rate of 900 cm3/s when the edge is 10 cm long.
Question 5:
A stone is dropped into a quiet lake and waves move in circles at the speed of 5 cm/s. At the instant when the radius of the circular wave is 8 cm, how fast is the enclosed area increasing?
Answer:
The area of a circle (A) with radius (r) is given by.
Therefore, the rate of change of area (A) with respect to time (t) is given by,
[By chain rule]
It is given that.
Thus, when r = 8 cm,
Hence, when the radius of the circular wave is 8 cm, the enclosed area is increasing at the rate of 80π cm2/s.
Page No 198:
Question 6:
The radius of a circle is increasing at the rate of 0.7 cm/s. What is the rate of increase of its circumference?
Answer:
The circumference of a circle (C) with radius (r) is given by
C = 2πr.
Therefore, the rate of change of circumference (C) with respect to time (t) is given by,
(By chain rule)
It is given that.
Hence, the rate of increase of the circumference
Question 7:
The length x of a rectangle is decreasing at the rate of 5 cm/minute and the width y is increasing at the rate of 4 cm/minute. When x = 8 cm and y = 6 cm, find the rates of change of (a) the perimeter, and (b) the area of the rectangle.
Answer:
Since the length (x) is decreasing at the rate of 5 cm/minute and the width (y) is increasing at the rate of 4 cm/minute, we have:
and
(a) The perimeter (P) of a rectangle is given by,
P = 2(x + y)
Hence, the perimeter is decreasing at the rate of 2 cm/min.
(b) The area (A) of a rectangle is given by,
A = x⋅ y
∴
When x = 8 cm and y = 6 cm,
Hence, the area of the rectangle is increasing at the rate of 2 cm2/min.
Question 8:
A balloon, which always remains spherical on inflation, is being inflated by pumping in 900 cubic centimetres of gas per second. Find the rate at which the radius of the balloon increases when the radius is 15 cm.
Answer:
The volume of a sphere (V) with radius (r) is given by,
∴Rate of change of volume (V) with respect to time (t) is given by,
[By chain rule]
It is given that.
Therefore, when radius = 15 cm,
Hence, the rate at which the radius of the balloon increases when the radius is 15 cm is
Question 9:
A balloon, which always remains spherical has a variable radius. Find the rate at which its volume is increasing with the radius when the later is 10 cm.
Answer:
The volume of a sphere (V) with radius (r) is given by.
Rate of change of volume (V) with respect to its radius (r) is given by,
Therefore, when radius = 10 cm,
Hence, the volume of the balloon is increasing at the rate of 400π cm2.
Question 10:
A ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2 cm/s. How fast is its height on the wall decreasing when the foot of the ladder is 4 m away from the wall?
Answer:
Let y m be the height of the wall at which the ladder touches. Also, let the foot of the ladder be x maway from the wall.
Then, by Pythagoras theorem, we have:
x2 + y2 = 25 [Length of the ladder = 5 m]
Then, the rate of change of height (y) with respect to time (t) is given by,
It is given that.
Now, when x = 4 m, we have:
Hence, the height of the ladder on the wall is decreasing at the rate of.
Question 11:
A particle moves along the curve. Find the points on the curve at which the y-coordinate is changing 8 times as fast as the x-coordinate.
Answer:
The equation of the curve is given as:
The rate of change of the position of the particle with respect to time (t) is given by,
When the y-coordinate of the particle changes 8 times as fast as the
x-coordinate i.e.,, we have:
When.
When.
Hence, the points required on the curve are (4, 11) and
Question 12:
The radius of an air bubble is increasing at the rate of cm/s. At what rate is the volume of the bubble increasing when the radius is 1 cm?
Answer:
The air bubble is in the shape of a sphere.
Now, the volume of an air bubble (V) with radius (r) is given by,
The rate of change of volume (V) with respect to time (t) is given by,
It is given that.
Therefore, when r = 1 cm,
Hence, the rate at which the volume of the bubble increases is 2π cm3/s.
Question 13:
A balloon, which always remains spherical, has a variable diameter Find the rate of change of its volume with respect to x.
Answer:
The volume of a sphere (V) with radius (r) is given by,
It is given that:
Diameter
Hence, the rate of change of volume with respect to x is as
Question 14:
Sand is pouring from a pipe at the rate of 12 cm3/s. The falling sand forms a cone on the ground in such a way that the height of the cone is always one-sixth of the radius of the base. How fast is the height of the sand cone increasing when the height is 4 cm?
Answer:
The volume of a cone (V) with radius (r) and height (h) is given by,
It is given that,
The rate of change of volume with respect to time (t) is given by,
[By chain rule]
It is also given that.
Therefore, when h = 4 cm, we have:
Hence, when the height of the sand cone is 4 cm, its height is increasing at the rate of.
Question 15:
The total cost C (x) in Rupees associated with the production of x units of an item is given by
Find the marginal cost when 17 units are produced.
Answer:
Marginal cost is the rate of change of total cost with respect to output.
∴Marginal cost (MC)
When x = 17, MC = 0.021 (172) − 0.006 (17) + 15
= 0.021(289) − 0.006(17) + 15
= 6.069 − 0.102 + 15
= 20.967
Hence, when 17 units are produced, the marginal cost is Rs. 20.967.
Question 16:
The total revenue in Rupees received from the sale of x units of a product is given by
Find the marginal revenue when x = 7.
Answer:
Marginal revenue is the rate of change of total revenue with respect to the number of units sold.
∴Marginal Revenue (MR) = 13(2x) + 26 = 26x + 26
When x = 7,
MR = 26(7) + 26 = 182 + 26 = 208
Hence, the required marginal revenue is Rs 208.
Question 17:
The rate of change of the area of a circle with respect to its radius r at r = 6 cm is
(A) 10π (B) 12π (C) 8π (D) 11π
Answer:
The area of a circle (A) with radius (r) is given by,
Therefore, the rate of change of the area with respect to its radius r is
.
∴When r = 6 cm,
Hence, the required rate of change of the area of a circle is 12π cm2/s.
The correct answer is B.
Page No 199:
Question 18:
The total revenue in Rupees received from the sale of x units of a product is given by
. The marginal revenue, when
is
(A) 116 (B) 96 (C) 90 (D) 126
Answer:
Marginal revenue is the rate of change of total revenue with respect to the number of units sold.
∴Marginal Revenue (MR)= 3(2x) + 36 = 6x + 36
∴When x = 15,
MR = 6(15) + 36 = 90 + 36 = 126
Hence, the required marginal revenue is Rs 126.
The correct answer is D.
Page No 205:
Question 1:
Show that the function given by f(x) = 3x + 17 is strictly increasing on R.
Answer:
Letbe any two numbers in R.
Then, we have:
Hence, f is strictly increasing on R.
Question 2:
Show that the function given by f(x) = e2x is strictly increasing on R.
Answer:
Letbe any two numbers in R.
Then, we have:
Hence, f is strictly increasing on R.
Question 3:
Show that the function given by f(x) = sin x is
(a) strictly increasing in (b) strictly decreasing in
(c) neither increasing nor decreasing in (0, π)
Answer:
The given function is f(x) = sin x.
(a) Since for eachwe have
.
Hence, f is strictly increasing in.
(b) Since for each, we have
.
Hence, f is strictly decreasing in.
(c) From the results obtained in (a) and (b), it is clear that f is neither increasing nor decreasing in (0, π).
Question 4:
Find the intervals in which the function f given by f(x) = 2x2 − 3x is
(a) strictly increasing (b) strictly decreasing
Answer:
The given function is f(x) = 2x2 − 3x.
Now, the pointdivides the real line into two disjoint intervals i.e.,
and
In interval
Hence, the given function (f) is strictly decreasing in interval.
In interval
Hence, the given function (f) is strictly increasing in interval.
Question 5:
Find the intervals in which the function f given by f(x) = 2x3 − 3x2 − 36x + 7 is
(a) strictly increasing (b) strictly decreasing
Answer:
The given function is f(x) = 2x3 − 3x2 − 36x + 7.
∴ x = − 2, 3
The points x = −2 and x = 3 divide the real line into three disjoint intervals i.e.,
In intervalsis positive while in interval
(−2, 3), is negative.
Hence, the given function (f) is strictly increasing in intervals
, while function (f) is strictly decreasing in interval
(−2, 3).
Question 6:
Find the intervals in which the following functions are strictly increasing or decreasing:
(a) x2 + 2x − 5 (b) 10 − 6x − 2x2
(c) −2x3 − 9x2 − 12x + 1 (d) 6 − 9x − x2
(e) (x + 1)3 (x − 3)3
Answer:
(a) We have,
Now,
x = −1
Point x = −1 divides the real line into two disjoint intervals i.e.,
In interval
∴f is strictly decreasing in interval
Thus, f is strictly decreasing for x < −1.
In interval
∴ f is strictly increasing in interval
Thus, f is strictly increasing for x > −1.
(b) We have,
f(x) = 10 − 6x − 2x2
The pointdivides the real line into two disjoint intervals i.e.,
In interval i.e., when
,
f'(x)=-6-4x>0.
∴ f is strictly increasing for .
In interval i.e., when
,
∴ f is strictly decreasing for .
(c) We have,
f(x) = −2x3 − 9x2 − 12x + 1
Points x = −1 and x = −2 divide the real line into three disjoint intervals i.e.,
In intervals i.e., when x < −2 and x > −1,
.
∴ f is strictly decreasing for x < −2 and x > −1.
Now, in interval (−2, −1) i.e., when −2 < x < −1, .
∴ f is strictly increasing for .
(d) We have,
The pointdivides the real line into two disjoint intervals i.e.,
.
In interval i.e., for
,
.
∴ f is strictly increasing for.
In interval i.e., for
,
∴ f is strictly decreasing for.
(e) We have,
f(x) = (x + 1)3 (x − 3)3
The points x = −1, x = 1, and x = 3 divide the real line into four disjoint intervals i.e.,, (−1, 1), (1, 3), and
.
In intervalsand (−1, 1),
.
∴ f is strictly decreasing in intervalsand (−1, 1).
In intervals (1, 3) and,
.
∴ f is strictly increasing in intervals (1, 3) and.
Question 7:
Show that, is an increasing function of x throughout its domain.
Answer:
We have,
∴
dydx=11+x-(2+x)(2)-2x(1)(2+x)2=11+x-4(2+x)2=x2(1+x)(2+x)2Now,
dydx=0
⇒x2(1+x)(2+x)2=0⇒x2=0 [(2+x)≠0 as x>-1]⇒x=0Since x > −1, point x = 0 divides the domain (−1, ∞) in two disjoint intervals i.e., −1 < x < 0 and x > 0.
When −1 < x < 0, we have:
x<0⇒x2>0x>-1⇒(2+x)>0⇒(2+x2)>0∴
y’=x2(1+x)(2+x)2>0Also, when x > 0:
x>0⇒x2>0, (2+x)2>0∴
y’=x2(1+x)(2+x)2>0Hence, function f is increasing throughout this domain.
Question 8:
Find the values of x for whichis an increasing function.
Answer:
We have,
The points x = 0, x = 1, and x = 2 divide the real line into four disjoint intervals i.e.,
In intervals,
.
∴ y is strictly decreasing in intervals .
However, in intervals (0, 1) and (2, ∞),
∴ y is strictly increasing in intervals (0, 1) and (2, ∞).
y is strictly increasing for 0 < x < 1 and x > 2.
Question 9:
Prove that is an increasing function of θ in
.
Answer:
We have,
Since cos θ ≠ 4, cos θ = 0.
Now,
In interval, we have cos θ > 0. Also, 4 > cos θ ⇒ 4 − cos θ > 0.
Therefore, y is strictly increasing in interval.
Also, the given function is continuous at
Hence, y is increasing in interval.
Page No 206:
Question 10:
Prove that the logarithmic function is strictly increasing on (0, ∞).
Answer:
It is clear that for x > 0,
Hence, f(x) = log x is strictly increasing in interval (0, ∞).
Question 11:
Prove that the function f given by f(x) = x2 − x + 1 is neither strictly increasing nor strictly decreasing on (−1, 1).
Answer:
The given function is f(x) = x2 − x + 1.
The pointdivides the interval (−1, 1) into two disjoint intervals i.e.,
Now, in interval
Therefore, f is strictly decreasing in interval.
However, in interval
Therefore, f is strictly increasing in interval.
Hence, f is neither strictly increasing nor decreasing in interval (−1, 1).
Question 12:
Which of the following functions are strictly decreasing on?
(A) cos x (B) cos 2x (C) cos 3x (D) tan x
Answer:
(A) Let
In interval
is strictly decreasing in interval
.
(B) Let
is strictly decreasing in interval
.
(C) Let
The point divides the interval
into two disjoint intervals
i.e., 0
∴ f3 is strictly increasing in interval.
Hence, f3 is neither increasing nor decreasing in interval.
(D) Let
In interval
∴ f4 is strictly increasing in interval
Therefore, functions cos x and cos 2x are strictly decreasing in
Hence, the correct answers are A and B.
Question 13:
On which of the following intervals is the function f given by strictly decreasing?
(A) (B)
(C) (D) None of these
Answer:
We have,
In interval
Thus, function f is strictly increasing in interval (0, 1).
In interval
Thus, function f is strictly increasing in interval.
∴ f is strictly increasing in interval.
Hence, function f is strictly decreasing in none of the intervals.
The correct answer is D.
Question 14:
Find the least value of a such that the function f given is strictly increasing on [1, 2].
Answer:
We have,
Now, function f is increasing on [1,2].
∴ f’x≥0 on 1,2Now, we have 1⩽x⩽2⇒2⩽2x⩽4⇒2+a⩽2x+a⩽4+a⇒2+a⩽f’x⩽4+aSince f’x≥0⇒2+a≥0⇒a≥-2So, least value of a is -2.
Question 15:
Let I be any interval disjoint from (−1, 1). Prove that the function f given by
is strictly increasing on I.
Answer:
We have,
The points x = 1 and x = −1 divide the real line in three disjoint intervals i.e., .
In interval (−1, 1), it is observed that:
∴ f is strictly decreasing on .
In intervals, it is observed that:
∴ f is strictly increasing on.
Hence, function f is strictly increasing in interval I disjoint from (−1, 1).
Hence, the given result is proved.
Question 16:
Prove that the function f given by f(x) = log sin x is strictly increasing on and strictly decreasing on
Answer:
We have,
In interval
∴ f is strictly increasing in.
In interval
∴f is strictly decreasing in
Question 17:
Prove that the function f given by f(x) = log cos x is strictly decreasing on and strictly increasing on
Answer:
We have,
In interval
∴f is strictly decreasing on.
In interval
∴f is strictly increasing on.
Question 18:
Prove that the function given by is increasing in R.
Answer:
We have,
For any x∈R, (x − 1)2 > 0.
Thus, is always positive in R.
Hence, the given function (f) is increasing in R.
Question 19:
The interval in which is increasing is
(A) (B) (−2, 0) (C)
(D) (0, 2)
Answer:
We have,
The points x = 0 and x = 2 divide the real line into three disjoint intervals i.e.,
In intervalsis always positive.
∴f is decreasing on
In interval (0, 2),
∴ f is strictly increasing on (0, 2).
Hence, f is strictly increasing in interval (0, 2).
The correct answer is D.
Page No 211:
Question 1:
Find the slope of the tangent to the curve y = 3x4 − 4x at x = 4.
Answer:
The given curve is y = 3x4 − 4x.
Then, the slope of the tangent to the given curve at x = 4 is given by,
Question 2:
Find the slope of the tangent to the curve, x ≠ 2 at x = 10.
Answer:
The given curve is.
Thus, the slope of the tangent at x = 10 is given by,
Hence, the slope of the tangent at x = 10 is
Question 3:
Find the slope of the tangent to curve y = x3 − x + 1 at the point whose x-coordinate is 2.
Answer:
The given curve is.
The slope of the tangent to a curve at (x, y) is.
It is given that x = 2.
Hence, the slope of the tangent at the point where the x-coordinate is 2 is given by,
Question 4:
Find the slope of the tangent to the curve y = x3 − 3x + 2 at the point whose x-coordinate is 3.
Answer:
The given curve is.
The slope of the tangent to a curve at (x, y) is.
Hence, the slope of the tangent at the point where the x-coordinate is 3 is given by,
Question 5:
Find the slope of the normal to the curve x = acos3θ, y = asin3θ at.
Answer:
It is given that x = acos3θ and y = asin3θ.
Therefore, the slope of the tangent at is given by,
Hence, the slope of the normal at
Question 6:
Find the slope of the normal to the curve x = 1 − a sin θ, y = b cos2θ at .
Answer:
It is given that x = 1 − a sin θ and y = b cos2θ.
Therefore, the slope of the tangent at is given by,
Hence, the slope of the normal at
Question 7:
Find points at which the tangent to the curve y = x3 − 3x2 − 9x + 7 is parallel to the x-axis.
Answer:
The equation of the given curve is
Now, the tangent is parallel to the x-axis if the slope of the tangent is zero.
When x = 3, y = (3)3 − 3 (3)2 − 9 (3) + 7 = 27 − 27 − 27 + 7 = −20.
When x = −1, y = (−1)3 − 3 (−1)2 − 9 (−1) + 7 = −1 − 3 + 9 + 7 = 12.
Hence, the points at which the tangent is parallel to the x-axis are (3, −20) and
(−1, 12).
Question 8:
Find a point on the curve y = (x − 2)2 at which the tangent is parallel to the chord joining the points (2, 0) and (4, 4).
Answer:
If a tangent is parallel to the chord joining the points (2, 0) and (4, 4), then the slope of the tangent = the slope of the chord.
The slope of the chord is
Now, the slope of the tangent to the given curve at a point (x, y) is given by,
Since the slope of the tangent = slope of the chord, we have:
Hence, the required point is (3, 1).
Page No 212:
Question 9:
Find the point on the curve y = x3 − 11x + 5 at which the tangent is y = x − 11.
Answer:
The equation of the given curve is y = x3 − 11x + 5.
The equation of the tangent to the given curve is given as y = x − 11 (which is of the form y = mx + c).
∴Slope of the tangent = 1
Now, the slope of the tangent to the given curve at the point (x, y) is given by,
Then, we have:
When x = 2, y = (2)3 − 11 (2) + 5 = 8 − 22 + 5 = −9.
When x = −2, y = (−2)3 − 11 (−2) + 5 = −8 + 22 + 5 = 19.
Hence, the required points are (2, −9) and (−2, 19). But, both these points should satisfy the equation of the tangent as there would be point of contact between tangent and the curve. ∴ (2, −9) is the required point as (−2, 19) is not satisfying the given equation of tangent.
Question 10:
Find the equation of all lines having slope −1 that are tangents to the curve .
Answer:
The equation of the given curve is.
The slope of the tangents to the given curve at any point (x, y) is given by,
If the slope of the tangent is −1, then we have:
When x = 0, y = −1 and when x = 2, y = 1.
Thus, there are two tangents to the given curve having slope −1. These are passing through the points (0, −1) and (2, 1).
∴The equation of the tangent through (0, −1) is given by,
∴The equation of the tangent through (2, 1) is given by,
y − 1 = −1 (x − 2)
⇒ y − 1 = − x + 2
⇒ y + x − 3 = 0
Hence, the equations of the required lines are y + x + 1 = 0 and y + x − 3 = 0.
Question 11:
Find the equation of all lines having slope 2 which are tangents to the curve.
Answer:
The equation of the given curve is.
The slope of the tangent to the given curve at any point (x, y) is given by,
If the slope of the tangent is 2, then we have:
Hence, there is no tangent to the given curve having slope 2.
Question 12:
Find the equations of all lines having slope 0 which are tangent to the curve .
Answer:
The equation of the given curve is.
The slope of the tangent to the given curve at any point (x, y) is given by,
If the slope of the tangent is 0, then we have:
When x = 1,
∴The equation of the tangent throughis given by,
Hence, the equation of the required line is
Question 13:
Find points on the curve at which the tangents are
(i) parallel to x-axis (ii) parallel to y-axis
Answer:
The equation of the given curve is.
On differentiating both sides with respect to x, we have:
(i) The tangent is parallel to the x-axis if the slope of the tangent is i.e., 0 which is possible if x = 0.
Then, for x = 0
Hence, the points at which the tangents are parallel to the x-axis are
(0, 4) and (0, − 4).
(ii) The tangent is parallel to the y-axis if the slope of the normal is 0, which gives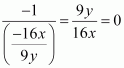
Then, for y = 0.
Hence, the points at which the tangents are parallel to the y-axis are
(3, 0) and (− 3, 0).
Question 14:
Find the equations of the tangent and normal to the given curves at the indicated points:
(i) y = x4 − 6x3 + 13x2 − 10x + 5 at (0, 5)
(ii) y = x4 − 6x3 + 13x2 − 10x + 5 at (1, 3)
(iii) y = x3 at (1, 1)
(iv) y = x2 at (0, 0)
(v) x = cos t, y = sin t at
Answer:
(i) The equation of the curve is y = x4 − 6x3 + 13x2 − 10x + 5.
On differentiating with respect to x, we get:
Thus, the slope of the tangent at (0, 5) is −10. The equation of the tangent is given as:
y − 5 = − 10(x − 0)
⇒ y − 5 = − 10x
⇒ 10x + y = 5
The slope of the normal at (0, 5) is
Therefore, the equation of the normal at (0, 5) is given as:
(ii) The equation of the curve is y = x4 − 6x3 + 13x2 − 10x + 5.
On differentiating with respect to x, we get:
Thus, the slope of the tangent at (1, 3) is 2. The equation of the tangent is given as:
The slope of the normal at (1, 3) is
Therefore, the equation of the normal at (1, 3) is given as:
(iii) The equation of the curve is y = x3.
On differentiating with respect to x, we get:
Thus, the slope of the tangent at (1, 1) is 3 and the equation of the tangent is given as:
The slope of the normal at (1, 1) is
Therefore, the equation of the normal at (1, 1) is given as:
(iv) The equation of the curve is y = x2.
On differentiating with respect to x, we get:
Thus, the slope of the tangent at (0, 0) is 0 and the equation of the tangent is given as:
y − 0 = 0 (x − 0)
⇒ y = 0
The slope of the normal at (0, 0) is , which is not defined.
Therefore, the equation of the normal at (x0, y) = (0, 0) is given by
(v) The equation of the curve is x = cos t, y = sin t.
∴The slope of the tangent atis −1.
When
Thus, the equation of the tangent to the given curve at 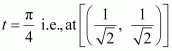
The slope of the normal atis
Therefore, the equation of the normal to the given curve at 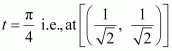
Question 15:
Find the equation of the tangent line to the curve y = x2 − 2x + 7 which is
(a) parallel to the line 2x − y + 9 = 0
(b) perpendicular to the line 5y − 15x = 13.
Answer:
The equation of the given curve is.
On differentiating with respect to x, we get:
(a) The equation of the line is 2x − y + 9 = 0.
2x − y + 9 = 0 ⇒ y = 2x + 9
This is of the form y = mx + c.
∴Slope of the line = 2
If a tangent is parallel to the line 2x − y + 9 = 0, then the slope of the tangent is equal to the slope of the line.
Therefore, we have:
2 = 2x − 2
Now, x = 2
y = 4 − 4 + 7 = 7
Thus, the equation of the tangent passing through (2, 7) is given by,
Hence, the equation of the tangent line to the given curve (which is parallel to line 2x − y + 9 = 0) is.
(b) The equation of the line is 5y − 15x = 13.
5y − 15x = 13 ⇒
This is of the form y = mx + c.
∴Slope of the line = 3
If a tangent is perpendicular to the line 5y − 15x = 13, then the slope of the tangent is
Thus, the equation of the tangent passing throughis given by,
Hence, the equation of the tangent line to the given curve (which is perpendicular to line 5y − 15x = 13) is.
Question 16:
Show that the tangents to the curve y = 7x3 + 11 at the points where x = 2 and x = −2 are parallel.
Answer:
The equation of the given curve is y = 7x3 + 11.
The slope of the tangent to a curve at (x, y) is. Therefore, the slope of the tangent at the point where x = 2 is given by,
It is observed that the slopes of the tangents at the points where x = 2 and x = −2 are equal.
Hence, the two tangents are parallel.
Question 17:
Find the points on the curve y = x3 at which the slope of the tangent is equal to the y-coordinate of the point.
Answer:
The equation of the given curve is y = x3.
The slope of the tangent at the point (x, y) is given by,
When the slope of the tangent is equal to the y-coordinate of the point, then y = 3x2.
Also, we have y = x3.
∴3x2 = x3
⇒ x2 (x − 3) = 0
⇒ x = 0, x = 3
When x = 0, then y = 0 and when x = 3, then y = 3(3)2 = 27.
Hence, the required points are (0, 0) and (3, 27).
Question 18:
For the curve y = 4x3 − 2x5, find all the points at which the tangents passes through the origin.
Answer:
The equation of the given curve is y = 4x3 − 2x5.
Therefore, the slope of the tangent at a point (x, y) is 12x2 − 10x4.
The equation of the tangent at (x, y) is given by,
When the tangent passes through the origin (0, 0), then X = Y = 0.
Therefore, equation (1) reduces to:
Also, we have
When x = 0, y =
When x = 1, y = 4 (1)3 − 2 (1)5 = 2.
When x = −1, y = 4 (−1)3 − 2 (−1)5 = −2.
Hence, the required points are (0, 0), (1, 2), and (−1, −2).
Question 19:
Find the points on the curve x2 + y2 − 2x − 3 = 0 at which the tangents are parallel to the x-axis.
Answer:
The equation of the given curve is x2 + y2 − 2x − 3 = 0.
On differentiating with respect to x, we have:
Now, the tangents are parallel to the x-axis if the slope of the tangent is 0.
But, x2 + y2 − 2x − 3 = 0 for x = 1.
y2 = 4 ⇒
Hence, the points at which the tangents are parallel to the x-axis are (1, 2) and (1, −2).
Question 20:
Find the equation of the normal at the point (am2, am3) for the curve ay2 = x3.
Answer:
The equation of the given curve is ay2 = x3.
On differentiating with respect to x, we have:
The slope of a tangent to the curve at (x, y) is.
The slope of the tangent to the given curve at (am2, am3) is
∴ Slope of normal at (am2, am3) =
Hence, the equation of the normal at (am2, am3) is given by,
y − am3 =
Page No 213:
Question 21:
Find the equation of the normals to the curve y = x3 + 2x + 6 which are parallel to the line x + 14y + 4 = 0.
Answer:
The equation of the given curve is y = x3 + 2x + 6.
The slope of the tangent to the given curve at any point (x, y) is given by,
∴ Slope of the normal to the given curve at any point (x, y) =
The equation of the given line is x + 14y + 4 = 0.
x + 14y + 4 = 0 ⇒ (which is of the form y = mx + c)
∴Slope of the given line =
If the normal is parallel to the line, then we must have the slope of the normal being equal to the slope of the line.
When x = 2, y = 8 + 4 + 6 = 18.
When x = −2, y = − 8 − 4 + 6 = −6.
Therefore, there are two normals to the given curve with slopeand passing through the points (2, 18) and (−2, −6).
Thus, the equation of the normal through (2, 18) is given by,
And, the equation of the normal through (−2, −6) is given by,
Hence, the equations of the normals to the given curve (which are parallel to the given line) are
Question 22:
Find the equations of the tangent and normal to the parabola y2 = 4ax at the point (at2, 2at).
Answer:
The equation of the given parabola is y2 = 4ax.
On differentiating y2 = 4ax with respect to x, we have:
∴The slope of the tangent atis
Then, the equation of the tangent atis given by,
y − 2at =
Now, the slope of the normal atis given by,
Thus, the equation of the normal at (at2, 2at) is given as:
Question 23:
Prove that the curves x = y2 and xy = k cut at right angles if 8k2 = 1. [Hint: Two curves intersect at right angle if the tangents to the curves at the point of intersection are perpendicular to each other.]
Answer:
The equations of the given curves are given as
Putting x = y2 in xy = k, we get:
Thus, the point of intersection of the given curves is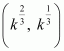
Differentiating x = y2 with respect to x, we have:
Therefore, the slope of the tangent to the curve x = y2 at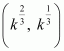
On differentiating xy = k with respect to x, we have:
∴ Slope of the tangent to the curve xy = k at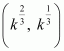
We know that two curves intersect at right angles if the tangents to the curves at the point of intersection i.e., at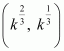
This implies that we should have the product of the tangents as − 1.
Thus, the given two curves cut at right angles if the product of the slopes of their respective tangents at 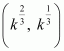
Hence, the given two curves cut at right angels if 8k2 = 1.
Question 24:
Find the equations of the tangent and normal to the hyperbola at the point
.
Answer:
Differentiatingwith respect to x, we have:
Therefore, the slope of the tangent atis
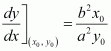
Then, the equation of the tangent atis given by,
Now, the slope of the normal atis given by,
Hence, the equation of the normal atis given by,
Question 25:
Find the equation of the tangent to the curve which is parallel to the line 4x − 2y + 5 = 0.
Answer:
The equation of the given curve is
The slope of the tangent to the given curve at any point (x, y) is given by,
The equation of the given line is 4x − 2y + 5 = 0.
4x − 2y + 5 = 0 ⇒ (which is of the form
∴Slope of the line = 2
Now, the tangent to the given curve is parallel to the line 4x − 2y − 5 = 0 if the slope of the tangent is equal to the slope of the line.
∴Equation of the tangent passing through the point is given by,
Hence, the equation of the required tangent is.
Question 26:
The slope of the normal to the curve y = 2x2 + 3 sin x at x = 0 is
(A) 3 (B) (C) −3 (D)
Answer:
The equation of the given curve is.
Slope of the tangent to the given curve at x = 0 is given by,
Hence, the slope of the normal to the given curve at x = 0 is
The correct answer is D.
Question 27:
The line y = x + 1 is a tangent to the curve y2 = 4x at the point
(A) (1, 2) (B) (2, 1) (C) (1, −2) (D) (−1, 2)
Answer:
The equation of the given curve is.
Differentiating with respect to x, we have:
Therefore, the slope of the tangent to the given curve at any point (x, y) is given by,
The given line is y = x + 1 (which is of the form y = mx + c)
∴ Slope of the line = 1
The line y = x + 1 is a tangent to the given curve if the slope of the line is equal to the slope of the tangent. Also, the line must intersect the curve.
Thus, we must have:
Hence, the line y = x + 1 is a tangent to the given curve at the point (1, 2).
The correct answer is A.
Page No 216:
Question 1:
1. Using differentials, find the approximate value of each of the following up to 3 places of decimal
(i) (ii)
(iii)
(iv) (v)
(vi)
(vii) (viii)
(ix)
(x) (xi)
(xii)
(xiii) (xiv)
(xv)
Answer:
(i)
Consider. Let x = 25 and Δx = 0.3.
Then,
Now, dy is approximately equal to Δy and is given by,
Hence, the approximate value ofis 0.03 + 5 = 5.03.
(ii)
Consider. Let x = 49 and Δx = 0.5.
Then,
Now, dy is approximately equal to Δy and is given by,
Hence, the approximate value ofis 7 + 0.035 = 7.035.
(iii)
Consider. Let x = 1 and Δx = − 0.4.
Then,
Now, dy is approximately equal to Δy and is given by,
Hence, the approximate value ofis 1 + (−0.2) = 1 − 0.2 = 0.8.
(iv)
Consider. Let x = 0.008 and Δx = 0.001.
Then,
Now, dy is approximately equal to Δy and is given by,
Hence, the approximate value ofis 0.2 + 0.008 = 0.208.
(v)
Consider. Let x = 1 and Δx = −0.001.
Then,
Now, dy is approximately equal to Δy and is given by,
Hence, the approximate value ofis 1 + (−0.0001) = 0.9999.
(vi)
Consider. Let x = 16 and Δx = −1.
Then,
Now, dy is approximately equal to Δy and is given by,
Hence, the approximate value ofis 2 + (−0.03125) = 1.96875.
(vii)
Consider. Let x = 27 and Δx = −1.
Then,
Now, dy is approximately equal to Δy and is given by,
Hence, the approximate value ofis 3 + (−0.0370) = 2.9629.
(viii)
Consider. Let x = 256 and Δx = −1.
Then,
Now, dy is approximately equal to Δy and is given by,
Hence, the approximate value ofis 4 + (−0.0039) = 3.9961.
(ix)
Consider. Let x = 81 and Δx = 1.
Then,
Now, dy is approximately equal to Δy and is given by,
Hence, the approximate value ofis 3 + 0.009 = 3.009.
(x)
Consider. Let x = 400 and Δx = 1.
Then,
Now, dy is approximately equal to Δy and is given by,
Hence, the approximate value ofis 20 + 0.025 = 20.025.
(xi)
Consider. Let x = 0.0036 and Δx = 0.0001.
Then,
Now, dy is approximately equal to Δy and is given by,
Thus, the approximate value ofis 0.06 + 0.00083 = 0.06083.
(xii)
Consider. Let x = 27 and Δx = −0.43.
Then,
Now, dy is approximately equal to Δy and is given by,
Hence, the approximate value ofis 3 + (−0.015) = 2.984.
(xiii)
Consider. Let x = 81 and Δx = 0.5.
Then,
Now, dy is approximately equal to Δy and is given by,
Hence, the approximate value ofis 3 + 0.0046 = 3.0046.
(xiv)
Consider. Let x = 4 and Δx = − 0.032.
Then,
Now, dy is approximately equal to Δy and is given by,
Hence, the approximate value ofis 8 + (−0.096) = 7.904.
(xv)
Consider. Let x = 32 and Δx = 0.15.
Then,
Now, dy is approximately equal to Δy and is given by,
Hence, the approximate value ofis 2 + 0.00187 = 2.00187.
Question 2:
Find the approximate value of f (2.01), where f (x) = 4x2 + 5x + 2
Answer:
Let x = 2 and Δx = 0.01. Then, we have:
f(2.01) = f(x + Δx) = 4(x + Δx)2 + 5(x + Δx) + 2
Now, Δy = f(x + Δx) − f(x)
∴ f(x + Δx) = f(x) + Δy
≈
Hence, the approximate value of f (2.01) is 28.21.
Question 3:
Find the approximate value of f (5.001), where f (x) = x3 − 7x2 + 15.
Answer:
Let x = 5 and Δx = 0.001. Then, we have:
Hence, the approximate value of f (5.001) is −34.995.
Question 4:
Find the approximate change in the volume V of a cube of side x metres caused by increasing side by 1%.
Answer:
The volume of a cube (V) of side x is given by V = x3.
Hence, the approximate change in the volume of the cube is 0.03x3 m3.
Question 5:
Find the approximate change in the surface area of a cube of side x metres caused by decreasing the side by 1%
Answer:
The surface area of a cube (S) of side x is given by S = 6x2.
Hence, the approximate change in the surface area of the cube is 0.12x2 m2.
Question 6:
If the radius of a sphere is measured as 7 m with an error of 0.02m, then find the approximate error in calculating its volume.
Answer:
Let r be the radius of the sphere and Δr be the error in measuring the radius.
Then,
r = 7 m and Δr = 0.02 m
Now, the volume V of the sphere is given by,
Hence, the approximate error in calculating the volume is 3.92 π m3.
Question 7:
If the radius of a sphere is measured as 9 m with an error of 0.03 m, then find the approximate error in calculating in surface area.
Answer:
Let r be the radius of the sphere and Δr be the error in measuring the radius.
Then,
r = 9 m and Δr = 0.03 m
Now, the surface area of the sphere (S) is given by,
S = 4πr2
Hence, the approximate error in calculating the surface area is 2.16π m2.
Question 8:
If f (x) = 3x2 + 15x + 5, then the approximate value of f (3.02) is
A. 47.66 B. 57.66 C. 67.66 D. 77.66
Answer:
Let x = 3 and Δx = 0.02. Then, we have:
Hence, the approximate value of f(3.02) is 77.66.
The correct answer is D.
Question 9:
The approximate change in the volume of a cube of side x metres caused by increasing the side by 3% is
A. 0.06 x3 m3 B. 0.6 x3 m3 C. 0.09 x3 m3 D. 0.9 x3 m3
Answer:
The volume of a cube (V) of side x is given by V = x3.
Hence, the approximate change in the volume of the cube is 0.09x3 m3.
The correct answer is C.
Page No 231:
Question 1:
Find the maximum and minimum values, if any, of the following functions given by
(i) f(x) = (2x − 1)2 + 3 (ii) f(x) = 9x2 + 12x + 2
(iii) f(x) = −(x − 1)2 + 10 (iv) g(x) = x3 + 1
Answer:
(i) The given function is f(x) = (2x − 1)2 + 3.
It can be observed that (2x − 1)2 ≥ 0 for every x ∈ R.
Therefore, f(x) = (2x − 1)2 + 3 ≥ 3 for every x ∈ R.
The minimum value of f is attained when 2x − 1 = 0.
2x − 1 = 0 ⇒
∴Minimum value of f == 3
Hence, function f does not have a maximum value.
(ii) The given function is f(x) = 9x2 + 12x + 2 = (3x + 2)2 − 2.
It can be observed that (3x + 2)2 ≥ 0 for every x ∈ R.
Therefore, f(x) = (3x + 2)2 − 2 ≥ −2 for every x ∈ R.
The minimum value of f is attained when 3x + 2 = 0.
3x + 2 = 0 ⇒
∴Minimum value of f =
Hence, function f does not have a maximum value.
(iii) The given function is f(x) = − (x − 1)2 + 10.
It can be observed that (x − 1)2 ≥ 0 for every x ∈ R.
Therefore, f(x) = − (x − 1)2 + 10 ≤ 10 for every x ∈ R.
The maximum value of f is attained when (x − 1) = 0.
(x − 1) = 0 ⇒ x = 1
∴Maximum value of f = f(1) = − (1 − 1)2 + 10 = 10
Hence, function f does not have a minimum value.
(iv) The given function is g(x) = x3 + 1.
Hence, function g neither has a maximum value nor a minimum value.
Page No 232:
Question 2:
Find the maximum and minimum values, if any, of the following functions given by
(i) f(x) = |x + 2| − 1 (ii) g(x) = − |x + 1| + 3
(iii) h(x) = sin(2x) + 5 (iv) f(x) = |sin 4x + 3|
(v) h(x) = x + 4, x (−1, 1)
Answer:
(i) f(x) =
We know that for every x ∈ R.
Therefore, f(x) = for every x ∈ R.
The minimum value of f is attained when.
∴Minimum value of f = f(−2) =
Hence, function f does not have a maximum value.
(ii) g(x) =
We know that for every x ∈ R.
Therefore, g(x) = for every x ∈ R.
The maximum value of g is attained when.
∴Maximum value of g = g(−1) =
Hence, function g does not have a minimum value.
(iii) h(x) = sin2x + 5
We know that − 1 ≤ sin 2x ≤ 1.
⇒ − 1 + 5 ≤ sin 2x + 5 ≤ 1 + 5
⇒ 4 ≤ sin 2x + 5 ≤ 6
Hence, the maximum and minimum values of h are 6 and 4 respectively.
(iv) f(x) =
We know that −1 ≤ sin 4x ≤ 1.
⇒ 2 ≤ sin 4x + 3 ≤ 4
⇒ 2 ≤≤ 4
Hence, the maximum and minimum values of f are 4 and 2 respectively.
(v) h(x) = x + 1, x ∈ (−1, 1)
Here, if a point x is closest to −1, then we find for all x ∈ (−1, 1).
Also, if x1 is closest to 1, then for all x1 ∈ (−1, 1).
Hence, function h(x) has neither maximum nor minimum value in (−1, 1).
Question 3:
Find the local maxima and local minima, if any, of the following functions. Find also the local maximum and the local minimum values, as the case may be:
(i). f(x) = x2 (ii). g(x) = x3 − 3x (iii). h(x) = sinx + cosx, 0 < (iv). f(x) = sinx − cos x, 0 < x < 2π
(v). f(x) = x3 − 6x2 + 9x + 15
(vi).
(vii).
(viii).
Answer:
(i) f(x) = x2
Thus, x = 0 is the only critical point which could possibly be the point of local maxima or local minima of f.
We have, which is positive.
Therefore, by second derivative test, x = 0 is a point of local minima and local minimum value of f at x = 0 is f(0) = 0.
(ii) g(x) = x3 − 3x
By second derivative test, x = 1 is a point of local minima and local minimum value of g at x = 1 is g(1) = 13 − 3 = 1 − 3 = −2. However,
x = −1 is a point of local maxima and local maximum value of g at
x = −1 is g(1) = (−1)3 − 3 (− 1) = − 1 + 3 = 2.
(iii) h(x) = sinx + cosx, 0 < x <
Therefore, by second derivative test, is a point of local maxima and the local maximum value of h at
is
(iv) f(x) = sin x − cos x, 0 < x < 2π ∴
f’x = cosx+sinx
f’x=0⇒cosx=-sinx⇒tanx=-1⇒x=3π4,7π4∈0,2π
f”x=-sinx+cosx
f”3π4=-sin3π4+cos3π4=-12-12=-2<0
f”7π4=-sin7π4+cos7π4=12+12=2>0Therefore, by second derivative test, is a point of local maxima and the local maximum value of f at
is
However,
is a point of local minima and the local minimum value of f at
is
.
(v) f(x) = x3 − 6x2 + 9x + 15
Therefore, by second derivative test, x = 1 is a point of local maxima and the local maximum value of f at x = 1 is f(1) = 1 − 6 + 9 + 15 = 19. However, x = 3 is a point of local minima and the local minimum value of f at x = 3 is f(3) = 27 − 54 + 27 + 15 = 15.
(vi)
Since x > 0, we take x = 2.
Therefore, by second derivative test, x = 2 is a point of local minima and the local minimum value of g at x = 2 is g(2) =
(vii)
Now, for values close to x = 0 and to the left of 0,Also, for values close to x = 0 and to the right of 0,
.
Therefore, by first derivative test, x = 0 is a point of local maxima and the local maximum value of.
(viii)
Therefore, by second derivative test,is a point of local maxima and the local maximum value of f at
is
Question 4:
Prove that the following functions do not have maxima or minima:
(i) f(x) = ex (ii) g(x) = logx
(iii) h(x) = x3 + x2 + x + 1
Answer:
- We have,
f(x) = ex
Now, if. But, the exponential function can never assume 0 for any value of x.
Therefore, there does not exist c∈ R such that
Hence, function f does not have maxima or minima.
- We have,
g(x) = log x
Therefore, there does not exist c∈ R such that.
Hence, function g does not have maxima or minima.
- We have,
h(x) = x3 + x2 + x + 1
Now,
h(x) = 0 ⇒ 3x2 + 2x + 1 = 0 ⇒
Therefore, there does not exist c∈ R such that.
Hence, function h does not have maxima or minima.
Question 5:
Find the absolute maximum value and the absolute minimum value of the following functions in the given intervals:
(i) (ii)
(iii)
(iv)
Answer:
(i) The given function is f(x) = x3.
Then, we evaluate the value of f at critical point x = 0 and at end points of the interval [−2, 2].
f(0) = 0
f(−2) = (−2)3 = −8
f(2) = (2)3 = 8
Hence, we can conclude that the absolute maximum value of f on [−2, 2] is 8 occurring at x = 2. Also, the absolute minimum value of f on [−2, 2] is −8 occurring at x = −2.
(ii) The given function is f(x) = sin x + cos x.
Then, we evaluate the value of f at critical point and at the end points of the interval [0, π].
Hence, we can conclude that the absolute maximum value of f on [0, π] is occurring at
and the absolute minimum value of f on [0, π] is −1 occurring at x = π.
(iii) The given function is
Then, we evaluate the value of f at critical point x = 4 and at the end points of the interval.
Hence, we can conclude that the absolute maximum value of f onis 8 occurring at x = 4 and the absolute minimum value of f on
is −10 occurring at x = −2.
(iv) The given function is
Now,
2(x − 1) = 0 ⇒ x = 1
Then, we evaluate the value of f at critical point x = 1 and at the end points of the interval [−3, 1].
Hence, we can conclude that the absolute maximum value of f on [−3, 1] is 19 occurring at x = −3 and the minimum value of f on [−3, 1] is 3 occurring at x = 1.
Question 6:
Find the maximum profit that a company can make, if the profit function is given by
p(x) = 41 − 72x − 18x2
Answer:
The profit function is given as p(x) = 41 − 72x − 18x2. ∴
p'(x)=-72-36x⇒x=-7236=-2
Also,
p”(-2)=-36<0
By second derivative test,
x=-2
is the point of local maxima of p.
∴
Maximum profit=p-2
=41-72(-2)-18(-2)2=41+144-72=113
Hence, the maximum profit that the company can make is 113 units.
Question 7:
Find both the maximum value and the minimum value of
3x4 − 8x3 + 12x2 − 48x + 25 on the interval [0, 3]
Answer:
Let f(x) = 3x4 − 8x3 + 12x2 − 48x + 25.
Now,gives x = 2 or x2+ 2 = 0 for which there are no real roots.
Therefore, we consider only x = 2 ∈[0, 3].
Now, we evaluate the value of f at critical point x = 2 and at the end points of the interval [0, 3].
Hence, we can conclude that the absolute maximum value of f on [0, 3] is 25 occurring at x = 0 and the absolute minimum value of f at [0, 3] is − 39 occurring at x = 2.
Question 8:
At what points in the interval [0, 2π], does the function sin 2x attain its maximum value?
Answer:
Let f(x) = sin 2x.
Then, we evaluate the values of f at critical pointsand at the end points of the interval [0, 2π].
Hence, we can conclude that the absolute maximum value of f on [0, 2π] is occurring atand
.
Question 9:
What is the maximum value of the function sin x + cos x?
Answer:
Let f(x) = sin x + cos x.
Now, will be negative when (sin x + cos x) is positive i.e., when sin x and cos x are both positive. Also, we know that sin x and cos x both are positive in the first quadrant. Then,
will be negative when
.
Thus, we consider.
∴By second derivative test, f will be the maximum atand the maximum value of f is
.
Question 10:
Find the maximum value of 2x3 − 24x + 107 in the interval [1, 3]. Find the maximum value of the same function in [−3, −1].
Answer:
Let f(x) = 2x3 − 24x + 107.
We first consider the interval [1, 3].
Then, we evaluate the value of f at the critical point x = 2 ∈ [1, 3] and at the end points of the interval [1, 3].
f(2) = 2(8) − 24(2) + 107 = 16 − 48 + 107 = 75
f(1) = 2(1) − 24(1) + 107 = 2 − 24 + 107 = 85
f(3) = 2(27) − 24(3) + 107 = 54 − 72 + 107 = 89
Hence, the absolute maximum value of f(x) in the interval [1, 3] is 89 occurring at x = 3.
Next, we consider the interval [−3, −1].
Evaluate the value of f at the critical point x = −2 ∈ [−3, −1] and at the end points of the interval [1, 3].
f(−3) = 2 (−27) − 24(−3) + 107 = −54 + 72 + 107 = 125
f(−1) = 2(−1) − 24 (−1) + 107 = −2 + 24 + 107 = 129
f(−2) = 2(−8) − 24 (−2) + 107 = −16 + 48 + 107 = 139
Hence, the absolute maximum value of f(x) in the interval [−3, −1] is 139 occurring at x = −2.
Page No 233:
Question 11:
It is given that at x = 1, the function x4− 62x2 + ax + 9 attains its maximum value, on the interval [0, 2]. Find the value of a.
Answer:
Let f(x) = x4 − 62x2 + ax + 9.
It is given that function f attains its maximum value on the interval [0, 2] at x = 1.
Hence, the value of a is 120.
Question 12:
Find the maximum and minimum values of x + sin 2x on [0, 2π].
Answer:
Let f(x) = x + sin 2x.
Then, we evaluate the value of f at critical points and at the end points of the interval [0, 2π].
Hence, we can conclude that the absolute maximum value of f(x) in the interval [0, 2π] is 2π occurring at x = 2π and the absolute minimum value of f(x) in the interval [0, 2π] is 0 occurring at x = 0.
Question 13:
Find two numbers whose sum is 24 and whose product is as large as possible.
Answer:
Let one number be x. Then, the other number is (24 − x).
Let P(x) denote the product of the two numbers. Thus, we have:
∴By second derivative test, x = 12 is the point of local maxima of P. Hence, the product of the numbers is the maximum when the numbers are 12 and 24 − 12 = 12.
Question 14:
Find two positive numbers x and y such that x + y = 60 and xy3 is maximum.
Answer:
The two numbers are x and y such that x + y = 60.
⇒ y = 60 − x
Let f(x) = xy3.
∴By second derivative test, x = 15 is a point of local maxima of f. Thus, function xy3 is maximum when x = 15 and y = 60 − 15 = 45.
Hence, the required numbers are 15 and 45.
Question 15:
Find two positive numbers x and y such that their sum is 35 and the product x2y5 is a maximum
Answer:
Let one number be x. Then, the other number is y = (35 − x).
Let P(x) = x2y5. Then, we have:
x = 0, x = 35, x = 10
When x = 35, and y = 35 − 35 = 0. This will make the product x2 y5 equal to 0.
When x = 0, y = 35 − 0 = 35 and the product x2y2 will be 0.
∴ x = 0 and x = 35 cannot be the possible values of x.
When x = 10, we have:
∴ By second derivative test, P(x) will be the maximum when x = 10 and y = 35 − 10 = 25.
Hence, the required numbers are 10 and 25.
Question 16:
Find two positive numbers whose sum is 16 and the sum of whose cubes is minimum.
Answer:
Let one number be x. Then, the other number is (16 − x).
Let the sum of the cubes of these numbers be denoted by S(x). Then,
Now,
∴ By second derivative test, x = 8 is the point of local minima of S.
Hence, the sum of the cubes of the numbers is the minimum when the numbers are 8 and 16 − 8 = 8.
Question 17:
A square piece of tin of side 18 cm is to made into a box without top, by cutting a square from each corner and folding up the flaps to form the box. What should be the side of the square to be cut off so that the volume of the box is the maximum possible?
Answer:
Let the side of the square to be cut off be x cm. Then, the length and the breadth of the box will be (18 − 2x) cm each and the height of the box is x cm.
Therefore, the volume V(x) of the box is given by,
V(x) = x(18 − 2x)2
x = 9 or x = 3
If x = 9, then the length and the breadth will become 0.
x ≠ 9.
x = 3.
Now,
By second derivative test, x = 3 is the point of maxima of V.
Hence, if we remove a square of side 3 cm from each corner of the square tin and make a box from the remaining sheet, then the volume of the box obtained is the largest possible.
Question 18:
A rectangular sheet of tin 45 cm by 24 cm is to be made into a box without top, by cutting off square from each corner and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is the maximum possible?
Answer:
Let the side of the square to be cut off be x cm. Then, the height of the box is x, the length is 45 − 2x, and the breadth is 24 − 2x.
Therefore, the volume V(x) of the box is given by,
Now,
x = 18 and x = 5
It is not possible to cut off a square of side 18 cm from each corner of the rectangular sheet. Thus, x cannot be equal to 18.
∴x = 5
Now,
By second derivative test, x = 5 is the point of maxima.
Hence, the side of the square to be cut off to make the volume of the box maximum possible is 5 cm.
Question 19:
Show that of all the rectangles inscribed in a given fixed circle, the square has the maximum area.
Answer:
Let a rectangle of length l and breadth b be inscribed in the given circle of radius a.
Then, the diagonal passes through the centre and is of length 2a cm.
Now, by applying the Pythagoras theorem, we have:
∴Area of the rectangle,
By the second derivative test, when
, then the area of the rectangle is the maximum.
Since, the rectangle is a square.
Hence, it has been proved that of all the rectangles inscribed in the given fixed circle, the square has the maximum area.
Question 20:
Show that the right circular cylinder of given surface and maximum volume is such that is heights is equal to the diameter of the base.
Answer:
Let r and h be the radius and height of the cylinder respectively.
Then, the surface area (S) of the cylinder is given by,
Let V be the volume of the cylinder. Then,
∴ By second derivative test, the volume is the maximum when.
Hence, the volume is the maximum when the height is twice the radius i.e., when the height is equal to the diameter.
Question 21:
Of all the closed cylindrical cans (right circular), of a given volume of 100 cubic centimetres, find the dimensions of the can which has the minimum surface area?
Answer:
Let r and h be the radius and height of the cylinder respectively.
Then, volume (V) of the cylinder is given by,
Surface area (S) of the cylinder is given by,
∴By second derivative test, the surface area is the minimum when the radius of the cylinder is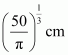
Hence, the required dimensions of the can which has the minimum surface area is given by radius = 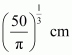
Question 22:
A wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the length of the two pieces so that the combined area of the square and the circle is minimum?
Answer:
Let a piece of length l be cut from the given wire to make a square.
Then, the other piece of wire to be made into a circle is of length (28 − l) m.
Now, side of square =.
Let r be the radius of the circle. Then,
The combined areas of the square and the circle (A) is given by,
Thus, when
By second derivative test, the area (A) is the minimum when
.
Hence, the combined area is the minimum when the length of the wire in making the square iscm while the length of the wire in making the circle is
.
Question 23:
Prove that the volume of the largest cone that can be inscribed in a sphere of radius R is of the volume of the sphere.
Answer:
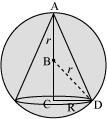
Let r and h be the radius and height of the cone respectively inscribed in a sphere of radius R.
Let V be the volume of the cone.
Then,
Height of the cone is given by,
h = R + AB
∴ By second derivative test, the volume of the cone is the maximum when
Question 24:
Show that the right circular cone of least curved surface and given volume has an altitude equal to time the radius of the base.
Answer:
Let r and h be the radius and the height (altitude) of the cone respectively.
Then, the volume (V) of the cone is given as:
V=13πr2h⇒h=3Vπr2The surface area (S) of the cone is given by,
S = πrl (where l is the slant height)
Thus, it can be easily verified that when
∴ By second derivative test, the surface area of the cone is the least when
Hence, for a given volume, the right circular cone of the least curved surface has an altitude equal to times the radius of the base.
Question 25:
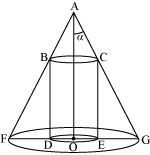
Show that the semi-vertical angle of the cone of the maximum volume and of given slant height is.
Answer:
Let θ be the semi-vertical angle of the cone.
It is clear that
Let r, h, and l be the radius, height, and the slant height of the cone respectively.
The slant height of the cone is given as constant.
Now, r = l sin θ and h = l cos θ
The volume (V) of the cone is given by,
∴By second derivative test, the volume (V) is the maximum when.
Hence, for a given slant height, the semi-vertical angle of the cone of the maximum volume is.
Question 26:
Show that semi-vertical angle of right circular cone of given surface area and maximum volume is .
Answer:
Let r be the radius, l be the slant height and h be the height of the cone of given surface area, S.
Also, let α be the semi-vertical angle of the cone.
Then S = πrl + πr2
Let V be the volume of the cone.
Differentiating (2) with respect to r, we get
For maximum or minimum, put
Differentiating again with respect to r, we get
Thus, V is maximum when S= 4πr2
As S = πrl + πr2
⇒ 4πr2 = πrl + πr2
⇒ 3πr2 = πrl
⇒ l = 3r
Now, in ΔCOB,
Page No 234:
Question 27:
The point on the curve x2 = 2y which is nearest to the point (0, 5) is
(A) (B)
(C) (0, 0) (D) (2, 2)
Answer:
The given curve is x2 = 2y.
For each value of x, the position of the point will be
Let P
x, x22 and A(0, 5) are the given points. Now distance between the points P and A is given by,
PA = x – 02 + x22 – 52⇒PA2 = x – 02 + x22 – 52⇒PA2 = x2 + x44 + 25 – 5×2⇒PA2 = x44 – 4×2 + 25⇒PA2 = y2 – 8y + 25 as, x2 = 2yLet us denote PA2 by Z. Then,
Z = y2 – 8y +25Differentiating both sides with respect to y, we get
dZdy = 2y – 8For maxima or minima, we have
dZdy = 0⇒2y – 8 = 0⇒y = 4d2Zdy2 = 2Now,d2Zdy2y=4 = 2 > 0Now, x2 = 2y ⇒x2 = 2×4⇒x2 = 8⇒x = 22 or x = -22So, Z is minimum at
22, 4 or -22, 4.
Or, PA2 is minimum at
22, 4 or -22, 4.
Or, PA is minimum at
22, 4 or -22, 4.
So, distance between the points
Px, x22 and A0, 5 is minimum at
22, 4 or -22, 4.
So, the correct answer is A.
Question 28:
For all real values of x, the minimum value of is
(A) 0 (B) 1
(C) 3 (D)
Answer:
Let
∴By second derivative test, f is the minimum at x = 1 and the minimum value is given by .
The correct answer is D.
Question 29:
The maximum value of is
(A) (B)
(C) 1 (D) 0
Answer:
Let
Then, we evaluate the value of f at critical pointand at the end points of the interval [0, 1] {i.e., at x = 0 and x = 1}.
Hence, we can conclude that the maximum value of f in the interval [0, 1] is 1.
The correct answer is C.
Page No 242:
Question 1:
Using differentials, find the approximate value of each of the following.
(a) (b)
Answer:
(a) Consider
Then,
Now, dy is approximately equal to Δy and is given by,
Hence, the approximate value of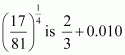
= 0.677.
(b) Consider. Let x = 32 and Δx = 1.
Then,
Now, dy is approximately equal to Δy and is given by,
Hence, the approximate value of
= 0.5 − 0.003 = 0.497.
Question 2:
Show that the function given byhas maximum at x = e.
Answer:
Now,
1 − log x = 0
Question 3:
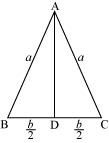
The two equal sides of an isosceles triangle with fixed base b are decreasing at the rate of 3 cm per second. How fast is the area decreasing when the two equal sides are equal to the base?
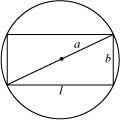
Answer:
Let ΔABC be isosceles where BC is the base of fixed length b.
Let the length of the two equal sides of ΔABC be a.
Draw AD⊥BC.
Now, in ΔADC, by applying the Pythagoras theorem, we have:
∴ Area of triangle
The rate of change of the area with respect to time (t) is given by,
It is given that the two equal sides of the triangle are decreasing at the rate of 3 cm per second.
∴
Then, when a = b, we have:
Hence, if the two equal sides are equal to the base, then the area of the triangle is decreasing at the rate of.
Question 4:
Find the equation of the normal to curve y2 = 4x at the point (1, 2).
Answer:
The equation of the given curve is.
Differentiating with respect to x, we have:
Now, the slope of the normal at point (1, 2) is
∴Equation of the normal at (1, 2) is y − 2 = −1(x − 1).
⇒ y − 2 = − x + 1
⇒ x + y − 3 = 0
Question 5:
Show that the normal at any point θ to the curve
is at a constant distance from the origin.
Answer:
We have x = a cos θ + a θ sin θ.
∴ Slope of the normal at any point θ is.
The equation of the normal at a given point (x, y) is given by,
Now, the perpendicular distance of the normal from the origin is
Hence, the perpendicular distance of the normal from the origin is constant.
Question 6:
Find the intervals in which the function f given by
is (i) increasing (ii) decreasing
Answer:
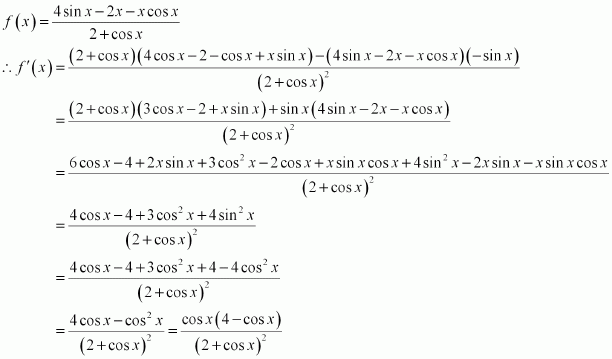
cos x = 0 or cos x = 4
But, cos x ≠ 4
∴cos x = 0
divides (0, 2π) into three disjoint intervals i.e.,
In intervals,
Thus, f(x) is increasing for
In the interval
Thus, f(x) is decreasing for.
Question 7:
Find the intervals in which the function f given byis
(i) increasing (ii) decreasing
Answer:
Now, the points x = 1 and x = −1 divide the real line into three disjoint intervals i.e.,
In intervals i.e., when x < −1 and x > 1,
Thus, when x < −1 and x > 1, f is increasing.
In interval (−1, 1) i.e., when −1 < x < 1,
Thus, when −1 < x < 1, f is decreasing.
Question 8:
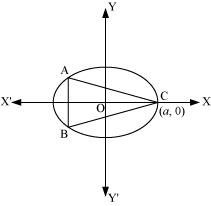
Find the maximum area of an isosceles triangle inscribed in the ellipse with its vertex at one end of the major axis.
Answer:
The given ellipse is.
Let the major axis be along the x −axis.
Let ABC be the triangle inscribed in the ellipse where vertex C is at (a, 0).
Since the ellipse is symmetrical with respect to the x−axis and y −axis, we can assume the coordinates of A to be (−x1, y1) and the coordinates of B to be (−x1, −y1).
Now, we have.
∴Coordinates of A are and the coordinates of B are
As the point (x1, y1) lies on the ellipse, the area of triangle ABC (A) is given by,
But, x1 cannot be equal to a.
Also, when, then
Thus, the area is the maximum when
∴ Maximum area of the triangle is given by,
Question 9:
A tank with rectangular base and rectangular sides, open at the top is to be constructed so that its depth is 2 m and volume is 8 m3. If building of tank costs Rs 70 per sq meters for the base and Rs 45 per square metre for sides. What is the cost of least expensive tank?
Answer:
Let l, b, and h represent the length, breadth, and height of the tank respectively.
Then, we have height (h) = 2 m
Volume of the tank = 8m3
Volume of the tank = l × b × h
∴ 8 = l × b × 2
Now, area of the base = lb = 4
Area of the 4 walls (A) = 2h (l + b)
However, the length cannot be negative.
Therefore, we have l = 4.
Thus, by second derivative test, the area is the minimum when l = 2.
We have l = b = h = 2.
∴Cost of building the base = Rs 70 × (lb) = Rs 70 (4) = Rs 280
Cost of building the walls = Rs 2h (l + b) × 45 = Rs 90 (2) (2 + 2)
= Rs 8 (90) = Rs 720
Required total cost = Rs (280 + 720) = Rs 1000
Hence, the total cost of the tank will be Rs 1000.
Question 10:
The sum of the perimeter of a circle and square is k, where k is some constant. Prove that the sum of their areas is least when the side of square is double the radius of the circle.
Answer:
Let r be the radius of the circle and a be the side of the square.
Then, we have:
The sum of the areas of the circle and the square (A) is given by,
Hence, it has been proved that the sum of their areas is least when the side of the square is double the radius of the circle.
Page No 243:
Question 11:
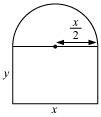
A window is in the form of rectangle surmounted by a semicircular opening. The total perimeter of the window is 10 m. Find the dimensions of the window to admit maximum light through the whole opening.
Answer:
Let x and y be the length and breadth of the rectangular window.
Radius of the semicircular opening
It is given that the perimeter of the window is 10 m.
∴Area of the window (A) is given by,
Thus, when
Therefore, by second derivative test, the area is the maximum when length.
Hence, the required dimensions of the window to admit maximum light is given by
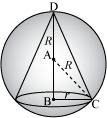
Question 12:
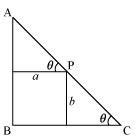
A point on the hypotenuse of a triangle is at distance a and b from the sides of the triangle.
Show that the minimum length of the hypotenuse is
Answer:
Let ΔABC be right-angled at B. Let AB = x and BC = y.
Let P be a point on the hypotenuse of the triangle such that P is at a distance of a and b from the sides AB and BC respectively.
Let ∠C = θ.
We have,
Now,
PC = b cosec θ
And, AP = a sec θ
∴AC = AP + PC
⇒ AC = b cosec θ + a sec θ … (1)
Therefore, by second derivative test, the length of the hypotenuse is the maximum when
Now, when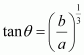
Hence, the maximum length of the hypotenuses is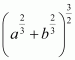
Question 13:
Find the points at which the function f given byhas
(i) local maxima (ii) local minima
(ii) point of inflexion
Answer:
The given function is
Now, for values of x close toand to the left of
Also, for values of x close to
and to the right of
Thus, is the point of local maxima.
Now, for values of x close to 2 and to the left of Also, for values of x close to 2 and to the right of 2,
Thus, x = 2 is the point of local minima.
Now, as the value of x varies through −1,does not changes its sign.
Thus, x = −1 is the point of inflexion.
Question 14:
Find the absolute maximum and minimum values of the function f given by
Answer:
Now, evaluating the value of f at critical pointsand at the end points of the interval
(i.e., at x = 0 and x = π), we have:
Hence, the absolute maximum value of f is occurring at
and the absolute minimum value of f is 1 occurring at
Question 15:
Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is.
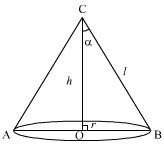
Answer:
A sphere of fixed radius (r) is given.
Let R and h be the radius and the height of the cone respectively.
The volume (V) of the cone is given by,
Now, from the right triangle BCD, we have:
∴h
∴ The volume is the maximum when
Hence, it can be seen that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is.
Question 16:
Let f be a function defined on [a, b] such that f ‘(x) > 0, for all x ∈ (a, b). Then prove that f is an increasing function on (a, b).
Answer:
Let
x1, x2∈(a,b)such that
x1<x2. Consider the sub-interval [
x1, x2]. Since f (x) is differentiable on (a, b) and
[x1, x2]⊂(a,b). Therefore, f(x) is continous on [
x1, x2] and differentiable on
(x1, x2). By the Lagrange’s mean value theorm, there exists
c∈(x1, x2)such that
f'(c)=f(x2)-f(x1)x2-x1 …(1)Since f‘(x) > 0 for all
x∈(a,b), so in particular, f‘(c) > 0
f'(c)>0⇒f(x2)-f(x1)x2-x1>0 [Using (1)]
⇒f(x2)-f(x1)>0 [∵
x2-x1>0 when x1<x2]
⇒f(x2)>f(x1)⇒f(x1)<f(x2)Since
x1, x2are arbitrary points in
(a,b). Therefore,
x1<x2⇒f(x1)<f(x2) for all x1,x2∈(a, b)Hence, f (x) is increasing on (a,b).
Question 17:
Show that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is. Also find the maximum volume.
Answer:
A sphere of fixed radius (R) is given.
Let r and h be the radius and the height of the cylinder respectively.
From the given figure, we have
The volume (V) of the cylinder is given by,
Now, it can be observed that at.
∴The volume is the maximum when
When, the height of the cylinder is
Hence, the volume of the cylinder is the maximum when the height of the cylinder is.
Question 18:
Show that height of the cylinder of greatest volume which can be inscribed in a right circular cone of height h and semi vertical angle α is one-third that of the cone and the greatest volume of cylinder istan2α.
Answer:
The given right circular cone of fixed height (h) and semi-vertical angle (α) can be drawn as:
Here, a cylinder of radius R and height H is inscribed in the cone.
Then, ∠GAO = α, OG = r, OA = h, OE = R, and CE = H.
We have,
r = h tan α
Now, since ΔAOG is similar to ΔCEG, we have:
Now, the volume (V) of the cylinder is given by,
And, for, we have:
∴By second derivative test, the volume of the cylinder is the greatest when
Thus, the height of the cylinder is one-third the height of the cone when the volume of the cylinder is the greatest.
Now, the maximum volume of the cylinder can be obtained as:
Hence, the given result is proved.
Question 19:
A cylindrical tank of radius 10 m is being filled with wheat at the rate of 314 cubic mere per hour. Then the depth of the wheat is increasing at the rate of
(A) 1 m/h (B) 0.1 m/h
(C) 1.1 m/h (D) 0.5 m/h
Answer:
Let r be the radius of the cylinder.
Then, volume (V) of the cylinder is given by,
Differentiating with respect to time t, we have:
The tank is being filled with wheat at the rate of 314 cubic metres per hour.
∴
Thus, we have:
Hence, the depth of wheat is increasing at the rate of 1 m/h.
The correct answer is A.
Question 20:
The slope of the tangent to the curveat the point (2, −1) is
(A) (B)
(C)
(D)
Answer:
The given curve is
The given point is (2, −1).
At x = 2, we have:
The common value of t is 2.
Hence, the slope of the tangent to the given curve at point (2, −1) is
The correct answer is B.
Page No 244:
Question 21:
The line y = mx + 1 is a tangent to the curve y2 = 4x if the value of m is
(A) 1 (B) 2 (C) 3 (D)
Answer:
The equation of the tangent to the given curve is y = mx + 1.
Now, substituting y = mx + 1 in y2 = 4x, we get:
Since a tangent touches the curve at one point, the roots of equation (i) must be equal.
Therefore, we have:
Hence, the required value of m is 1.
The correct answer is A.
Question 22:
The normal at the point (1, 1) on the curve 2y + x2 = 3 is
(A) x + y = 0 (B) x − y = 0
(C) x + y + 1 = 0 (D) x − y = 1
Answer:
The equation of the given curve is 2y + x2 = 3.
Differentiating with respect to x, we have:
The slope of the normal to the given curve at point (1, 1) is
Hence, the equation of the normal to the given curve at (1, 1) is given as:
The correct answer is B.
Question 23:
The normal to the curve x2 = 4y passing (1, 2) is
(A) x + y = 3 (B) x − y = 3
(C) x + y = 1 (D) x − y = 1
Answer:
The equation of the given curve is x2 = 4y.
Differentiating with respect to x, we have:
The slope of the normal to the given curve at point (h, k) is given by,
∴Equation of the normal at point (h, k) is given as:
Now, it is given that the normal passes through the point (1, 2).
Therefore, we have:
Since (h, k) lies on the curve x2 = 4y, we have h2 = 4k.
From equation (i), we have:
Hence, the equation of the normal is given as:
The correct answer is A.
Question 24:
The points on the curve 9y2 = x3, where the normal to the curve makes equal intercepts with the axes are
(A) (B)
(C) (D)
Answer:
The equation of the given curve is 9y2 = x3.
Differentiating with respect to x, we have:
The slope of the normal to the given curve at point is
∴ The equation of the normal to the curve at is
It is given that the normal makes equal intercepts with the axes.
Therefore, We have:
Also, the pointlies on the curve, so we have
From (i) and (ii), we have:
From (ii), we have:
Hence, the required points are
The correct answer is A.