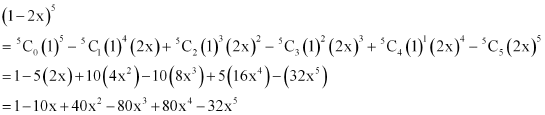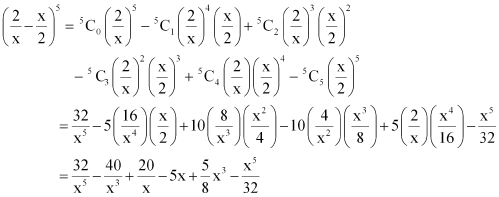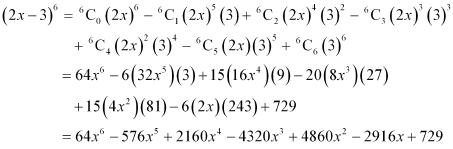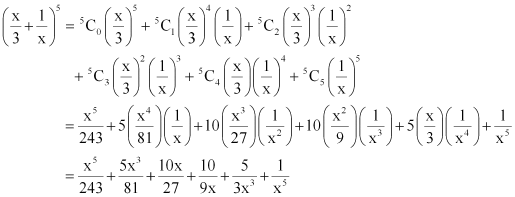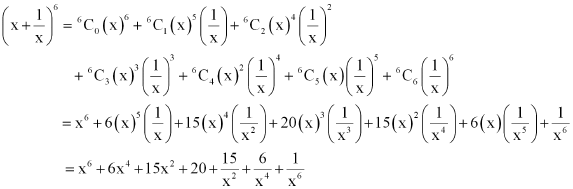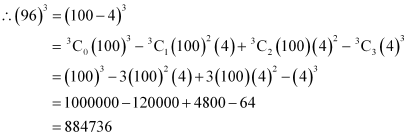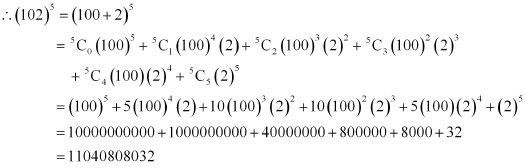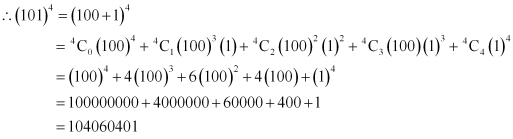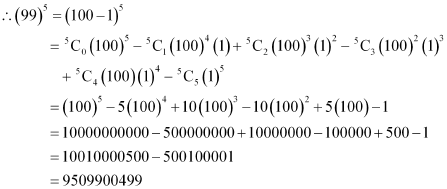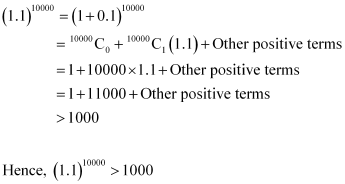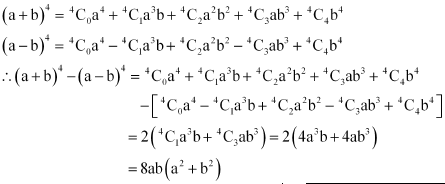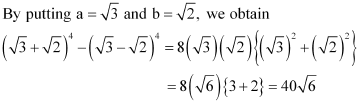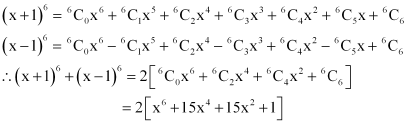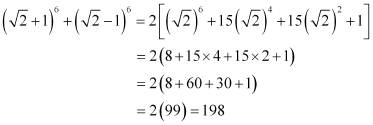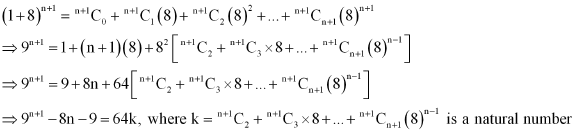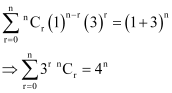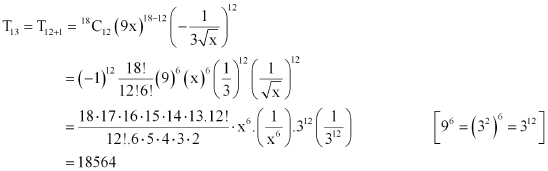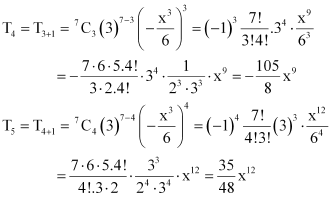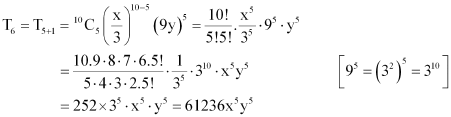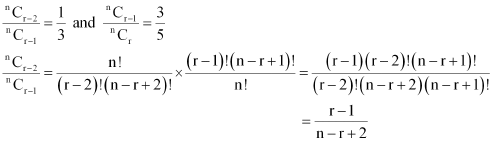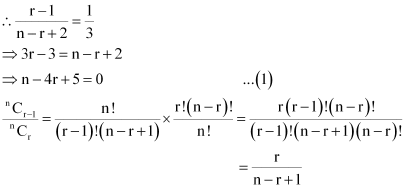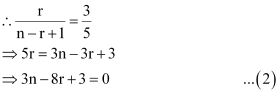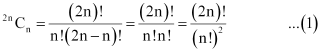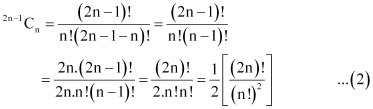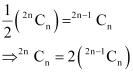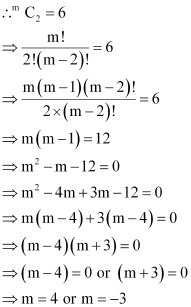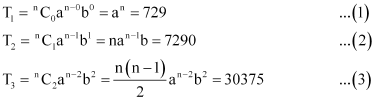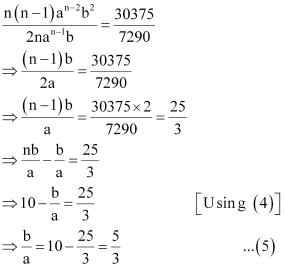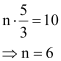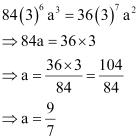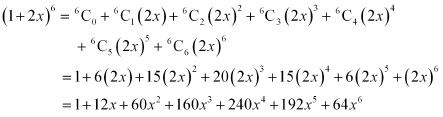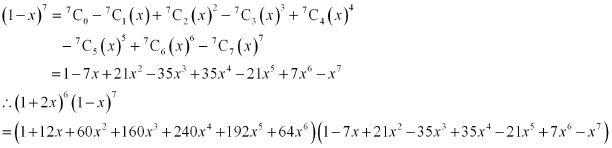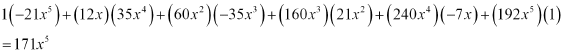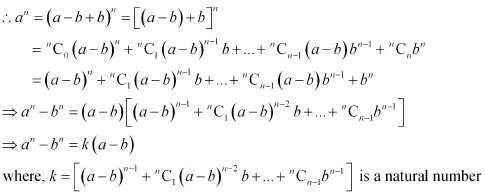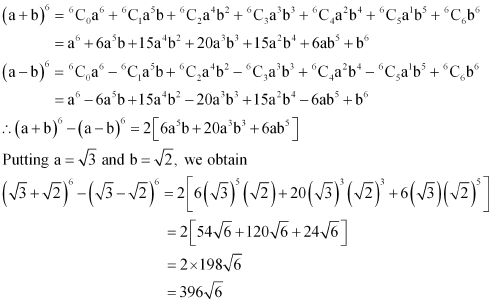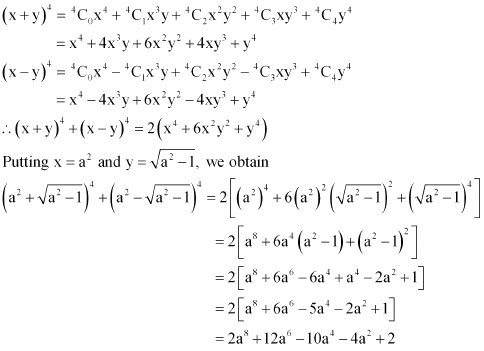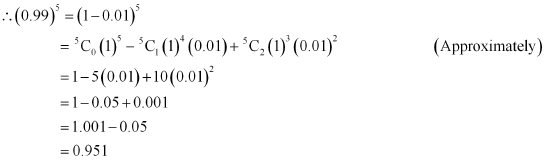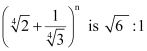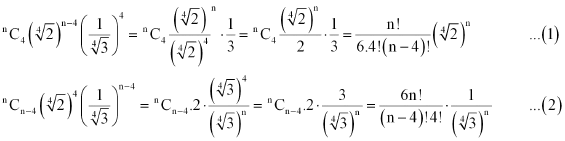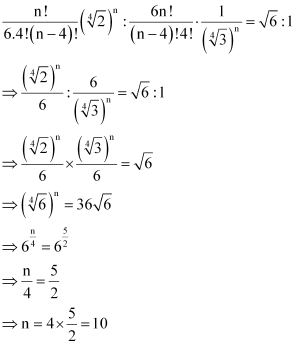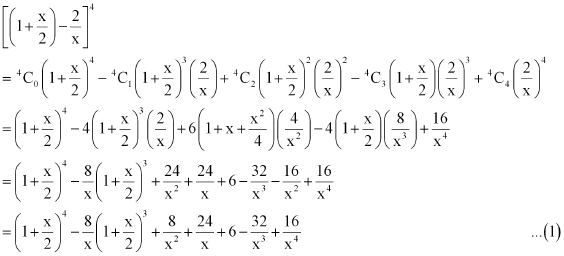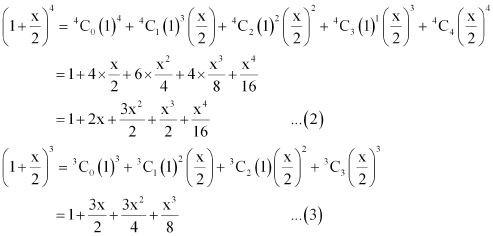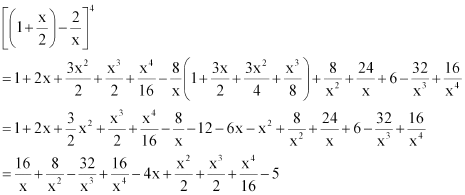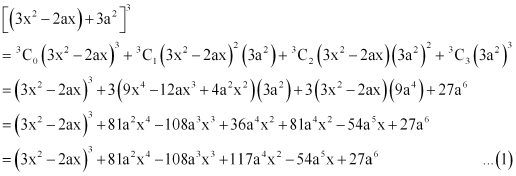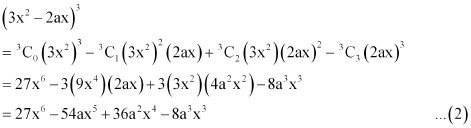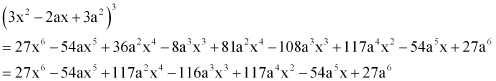NCERT Solutions for Class 11 Maths Chapter 8 – Binomial Theorem
Page No 166:
Question 1:
Expand the expression (1– 2x)5
ANSWER:
By using Binomial Theorem, the expression (1– 2x)5 can be expanded as
Page No 166:
Question 2:
Expand the expression
ANSWER:
By using Binomial Theorem, the expression can be expanded as
Page No 166:
Question 3:
Expand the expression (2x – 3)6
ANSWER:
By using Binomial Theorem, the expression (2x – 3)6 can be expanded as
Page No 167:
Question 4:
Expand the expression
ANSWER:
By using Binomial Theorem, the expression can be expanded as
Page No 167:
Question 5:
Expand
ANSWER:
By using Binomial Theorem, the expression can be expanded as
Page No 167:
Question 6:
Using Binomial Theorem, evaluate (96)3
ANSWER:
96 can be expressed as the sum or difference of two numbers whose powers are easier to calculate and then, binomial theorem can be applied.
It can be written that, 96 = 100 – 4
Page No 167:
Question 7:
Using Binomial Theorem, evaluate (102)5
ANSWER:
102 can be expressed as the sum or difference of two numbers whose powers are easier to calculate and then, Binomial Theorem can be applied.
It can be written that, 102 = 100 + 2
Page No 167:
Question 8:
Using Binomial Theorem, evaluate (101)4
ANSWER:
101 can be expressed as the sum or difference of two numbers whose powers are easier to calculate and then, Binomial Theorem can be applied.
It can be written that, 101 = 100 + 1
Page No 167:
Question 9:
Using Binomial Theorem, evaluate (99)5
ANSWER:
99 can be written as the sum or difference of two numbers whose powers are easier to calculate and then, Binomial Theorem can be applied.
It can be written that, 99 = 100 – 1
Page No 167:
Question 10:
Using Binomial Theorem, indicate which number is larger (1.1)10000 or 1000.
ANSWER:
By splitting 1.1 and then applying Binomial Theorem, the first few terms of (1.1)10000 can be obtained as
Page No 167:
Question 11:
Find (a + b)4 – (a – b)4. Hence, evaluate.
ANSWER:
Using Binomial Theorem, the expressions, (a + b)4 and (a – b)4, can be expanded as
Page No 167:
Question 12:
Find (x + 1)6 + (x – 1)6. Hence or otherwise evaluate.
ANSWER:
Using Binomial Theorem, the expressions, (x + 1)6 and (x – 1)6, can be expanded as
By putting, we obtain
Page No 167:
Question 13:
Show that is divisible by 64, whenever n is a positive integer.
ANSWER:
In order to show that is divisible by 64, it has to be proved that,
, where k is some natural number
By Binomial Theorem,
For a = 8 and m = n + 1, we obtain
Thus, is divisible by 64, whenever n is a positive integer.
Page No 167:
Question 14:
Prove that.
ANSWER:
By Binomial Theorem,
By putting b = 3 and a = 1 in the above equation, we obtain
Hence, proved.
Page No 171:
Question 1:
Find the coefficient of x5 in (x + 3)8
ANSWER:
It is known that (r + 1)th term, (Tr+1), in the binomial expansion of (a + b)n is given by .
Assuming that x5 occurs in the (r + 1)th term of the expansion (x + 3)8, we obtain
Comparing the indices of x in x5 and in Tr +1, we obtain
r = 3
Thus, the coefficient of x5 is
Page No 171:
Question 2:
Find the coefficient of a5b7 in (a – 2b)12
ANSWER:
It is known that (r + 1)th term, (Tr+1), in the binomial expansion of (a + b)n is given by .
Assuming that a5b7 occurs in the (r + 1)th term of the expansion (a – 2b)12, we obtain
Comparing the indices of a and b in a5 b7 and in Tr +1, we obtain
r = 7
Thus, the coefficient of a5b7 is
Page No 171:
Question 3:
Write the general term in the expansion of (x2 – y)6
ANSWER:
It is known that the general term Tr+1 {which is the (r + 1)th term} in the binomial expansion of (a + b)n is given by .
Thus, the general term in the expansion of (x2 – y6) is
Page No 171:
Question 4:
Write the general term in the expansion of (x2 – yx)12, x ≠ 0
ANSWER:
It is known that the general term Tr+1 {which is the (r + 1)th term} in the binomial expansion of (a + b)n is given by .
Thus, the general term in the expansion of(x2 – yx)12 is
Page No 171:
Question 5:
Find the 4th term in the expansion of (x – 2y)12 .
ANSWER:
It is known that (r + 1)th term, (Tr+1), in the binomial expansion of (a + b)n is given by .
Thus, the 4th term in the expansion of (x – 2y)12 is
Page No 171:
Question 6:
Find the 13th term in the expansion of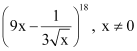
ANSWER:
It is known that (r + 1)th term, (Tr+1), in the binomial expansion of (a + b)n is given by .
Thus, 13th term in the expansion of 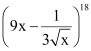
Page No 171:
Question 7:
Find the middle terms in the expansions of
ANSWER:
It is known that in the expansion of (a + b)n, if n is odd, then there are two middle terms, namely, term and
term.
Therefore, the middle terms in the expansion of 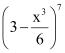
term and
term
Thus, the middle terms in the expansion of 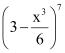
.
Page No 171:
Question 8:
Find the middle terms in the expansions of
ANSWER:
It is known that in the expansion (a + b)n, if n is even, then the middle term is term.
Therefore, the middle term in the expansion of is
term
Thus, the middle term in the expansion of is 61236 x5y5.
Page No 171:
Question 9:
In the expansion of (1 + a)m + n, prove that coefficients of am and an are equal.
ANSWER:
It is known that (r + 1)th term, (Tr+1), in the binomial expansion of (a + b)n is given by .
Assuming that am occurs in the (r + 1)th term of the expansion (1 + a)m + n, we obtain
Comparing the indices of a in am and in Tr + 1, we obtain
r = m
Therefore, the coefficient of am is
Assuming that an occurs in the (k + 1)th term of the expansion (1 + a)m+n, we obtain
Comparing the indices of a in an and in Tk + 1, we obtain
k = n
Therefore, the coefficient of an is
Thus, from (1) and (2), it can be observed that the coefficients of am and an in the expansion of (1 + a)m + n are equal.
Page No 171:
Question 10:
The coefficients of the (r – 1)th, rth and (r + 1)th terms in the expansion of
(x + 1)n are in the ratio 1:3:5. Find n and r.
ANSWER:
It is known that (k + 1)th term, (Tk+1), in the binomial expansion of (a + b)n is given by .
Therefore, (r – 1)th term in the expansion of (x + 1)n is
r th term in the expansion of (x + 1)n is
(r + 1)th term in the expansion of (x + 1)n is
Therefore, the coefficients of the (r – 1)th, rth, and (r + 1)th terms in the expansion of (x + 1)n are respectively. Since these coefficients are in the ratio 1:3:5, we obtain
Multiplying (1) by 3 and subtracting it from (2), we obtain
4r – 12 = 0
⇒ r = 3
Putting the value of r in (1), we obtain
n – 12 + 5 = 0
⇒ n = 7
Thus, n = 7 and r = 3
Page No 171:
Question 11:
Prove that the coefficient of xn in the expansion of (1 + x)2n is twice the coefficient of xn in the expansion of (1 + x)2n–1 .
ANSWER:
It is known that (r + 1)th term, (Tr+1), in the binomial expansion of (a + b)n is given by .
Assuming that xn occurs in the (r + 1)th term of the expansion of (1 + x)2n, we obtain
Comparing the indices of x in xn and in Tr + 1, we obtain
r = n
Therefore, the coefficient of xn in the expansion of (1 + x)2n is
Assuming that xn occurs in the (k +1)th term of the expansion (1 + x)2n – 1, we obtain
Comparing the indices of x in xn and Tk + 1, we obtain
k = n
Therefore, the coefficient of xn in the expansion of (1 + x)2n –1 is
From (1) and (2), it is observed that
Therefore, the coefficient of xn in the expansion of (1 + x)2n is twice the coefficient of xn in the expansion of (1 + x)2n–1.
Hence, proved.
Page No 171:
Question 12:
Find a positive value of m for which the coefficient of x2 in the expansion
(1 + x)m is 6.
ANSWER:
It is known that (r + 1)th term, (Tr+1), in the binomial expansion of (a + b)n is given by .
Assuming that x2 occurs in the (r + 1)th term of the expansion (1 +x)m, we obtain
Comparing the indices of x in x2 and in Tr + 1, we obtain
r = 2
Therefore, the coefficient of x2 is.
It is given that the coefficient of x2 in the expansion (1 + x)m is 6.
Thus, the positive value of m, for which the coefficient of x2 in the expansion
(1 + x)m is 6, is 4.
Page No 175:
Question 1:
Find a, b and n in the expansion of (a + b)n if the first three terms of the expansion are 729, 7290 and 30375, respectively.
ANSWER:
It is known that (r + 1)th term, (Tr+1), in the binomial expansion of (a + b)n is given by .
The first three terms of the expansion are given as 729, 7290, and 30375 respectively.
Therefore, we obtain
Dividing (2) by (1), we obtain
Dividing (3) by (2), we obtain
From (4) and (5), we obtain
Substituting n = 6 in equation (1), we obtain
a6 = 729
From (5), we obtain
Thus, a = 3, b = 5, and n = 6.
Page No 175:
Question 2:
Find a if the coefficients of x2 and x3 in the expansion of (3 + ax)9 are equal.
ANSWER:
It is known that (r + 1)th term, (Tr+1), in the binomial expansion of (a + b)n is given by .
Assuming that x2 occurs in the (r + 1)th term in the expansion of (3 + ax)9, we obtain
Comparing the indices of x in x2 and in Tr + 1, we obtain
r = 2
Thus, the coefficient of x2 is
Assuming that x3 occurs in the (k + 1)th term in the expansion of (3 + ax)9, we obtain
Comparing the indices of x in x3 and in Tk+ 1, we obtain
k = 3
Thus, the coefficient of x3 is
It is given that the coefficients of x2 and x3 are the same.
Thus, the required value of a is.
Page No 175:
Question 3:
Find the coefficient of x5 in the product (1 + 2x)6 (1 – x)7 using binomial theorem.
ANSWER:
Using Binomial Theorem, the expressions, (1 + 2x)6 and (1 – x)7, can be expanded as
The complete multiplication of the two brackets is not required to be carried out. Only those terms, which involve x5, are required.
The terms containing x5 are
Thus, the coefficient of x5 in the given product is 171.
Page No 175:
Question 4:
If a and b are distinct integers, prove that a – b is a factor of an – bn, whenever n is a positive integer.
[Hint: write an = (a – b + b)n and expand]
ANSWER:
In order to prove that (a – b) is a factor of (an – bn), it has to be proved that
an – bn = k (a – b), where k is some natural number
It can be written that, a = a – b + b
This shows that (a – b) is a factor of (an – bn), where n is a positive integer.
Page No 175:
Question 5:
Evaluate.
ANSWER:
Firstly, the expression (a + b)6 – (a – b)6 is simplified by using Binomial Theorem.
This can be done as
Page No 175:
Question 6:
Find the value of.
ANSWER:
Firstly, the expression (x + y)4 + (x – y)4 is simplified by using Binomial Theorem.
This can be done as
Page No 175:
Question 7:
Find an approximation of (0.99)5 using the first three terms of its expansion.
ANSWER:
0.99 = 1 – 0.01
Thus, the value of (0.99)5 is approximately 0.951.
Page No 175:
Question 8:
Find n, if the ratio of the fifth term from the beginning to the fifth term from the end in the expansion of
ANSWER:
In the expansion, ,
Fifth term from the beginning
Fifth term from the end
Therefore, it is evident that in the expansion of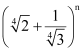
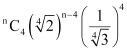
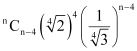
It is given that the ratio of the fifth term from the beginning to the fifth term from the end is. Therefore, from (1) and (2), we obtain
Thus, the value of n is 10.
Page No 176:
Question 9:
Expand using Binomial Theorem.
ANSWER:
Using Binomial Theorem, the given expression can be expanded as
Again by using Binomial Theorem, we obtain
From (1), (2), and (3), we obtain
Page No 176:
Question 10:
Find the expansion of using binomial theorem.
ANSWER:
Using Binomial Theorem, the given expression can be expanded as
Again by using Binomial Theorem, we obtain
From (1) and (2), we obtain