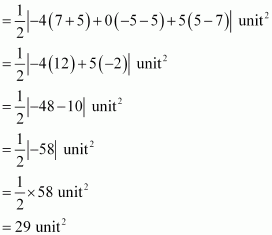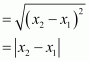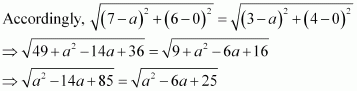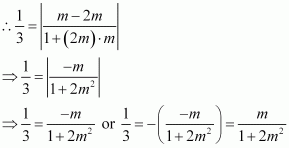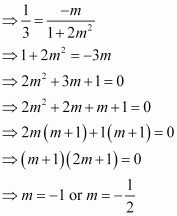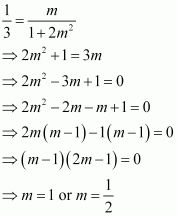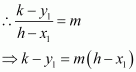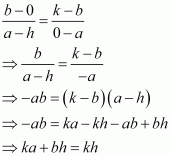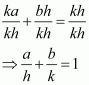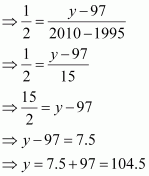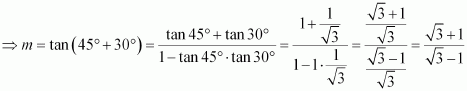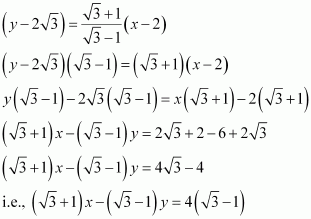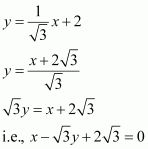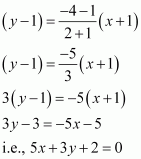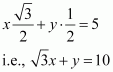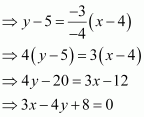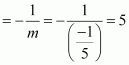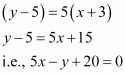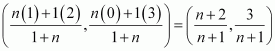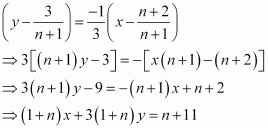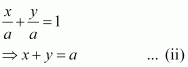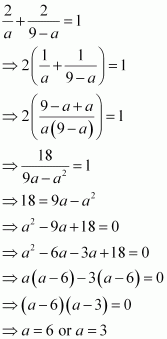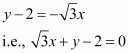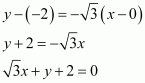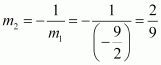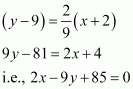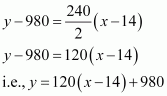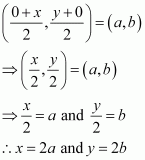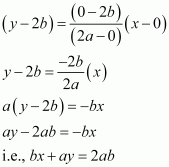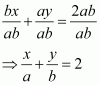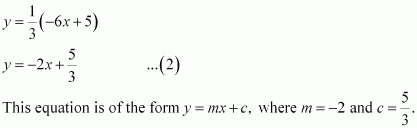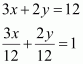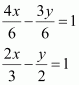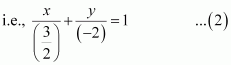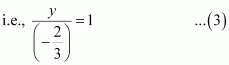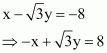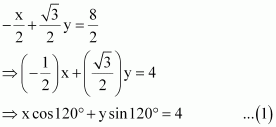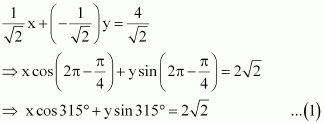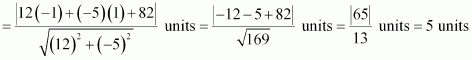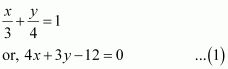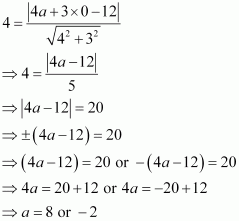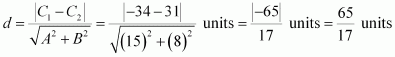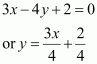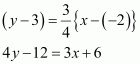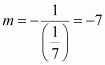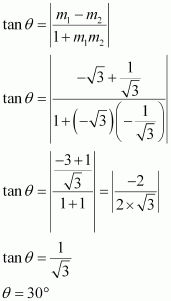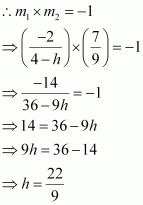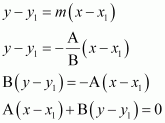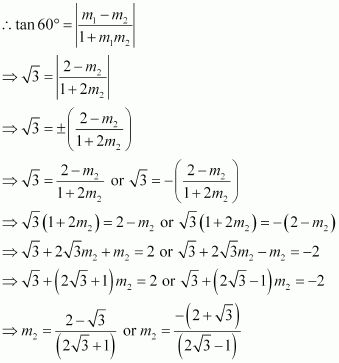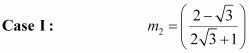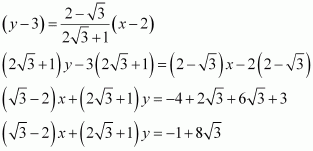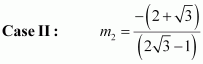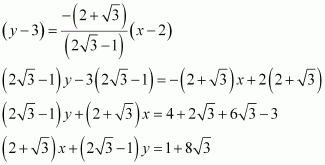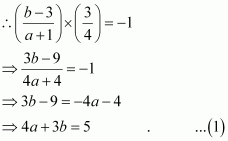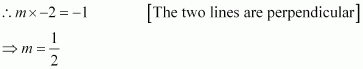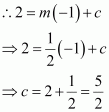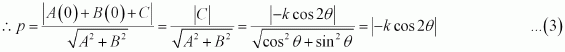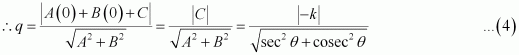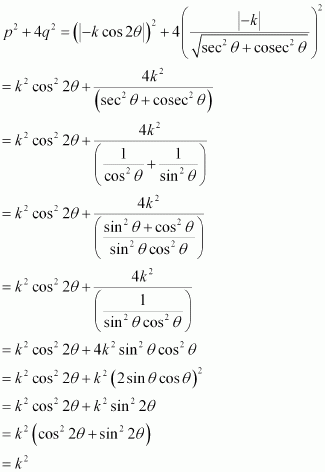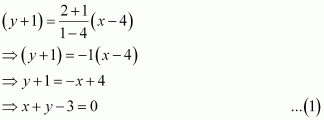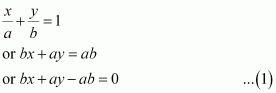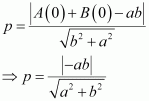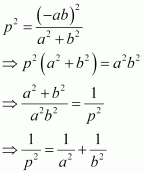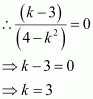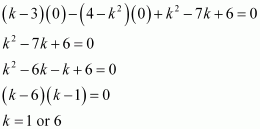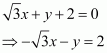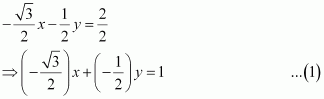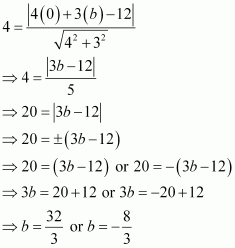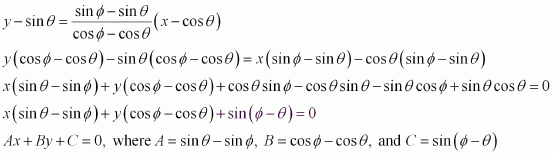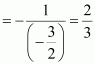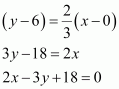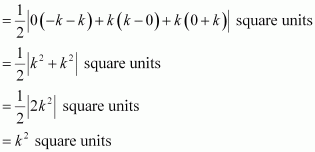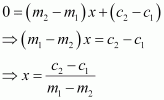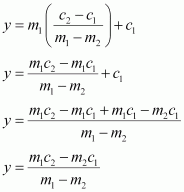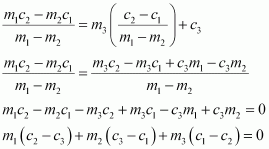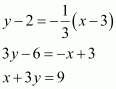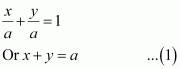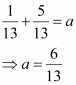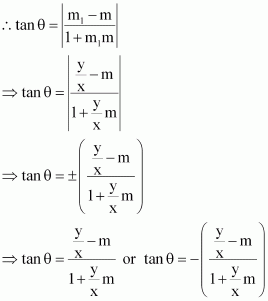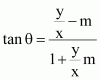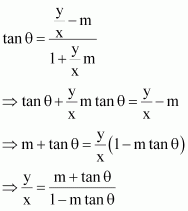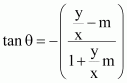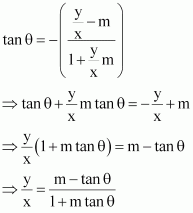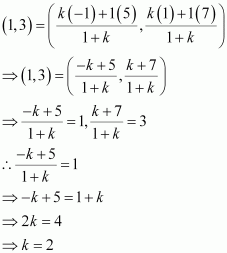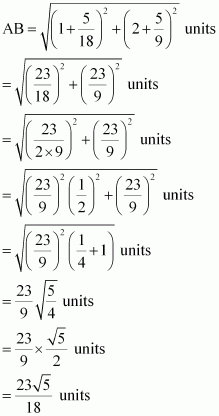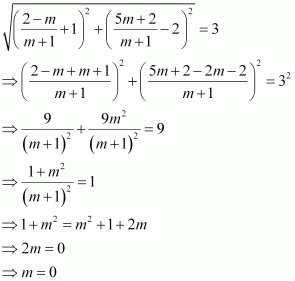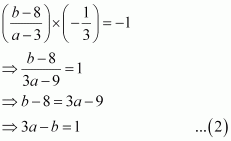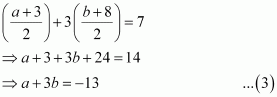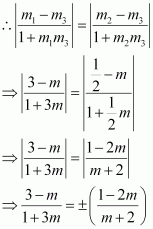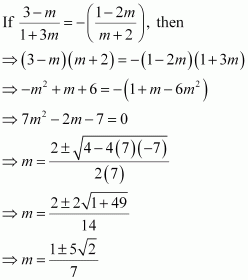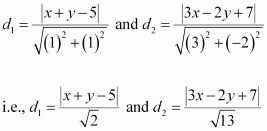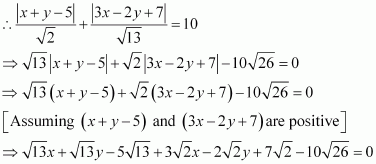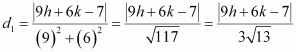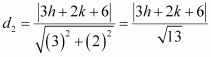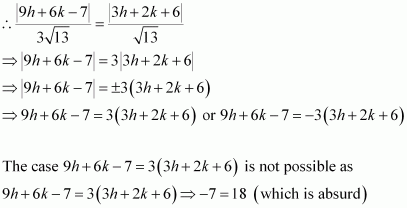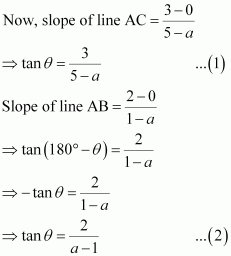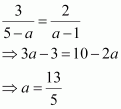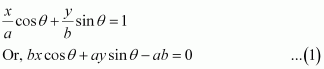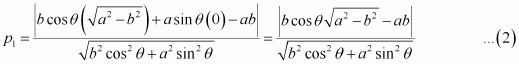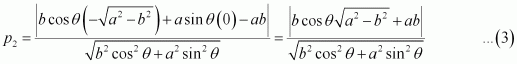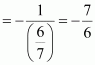NCERT Solutions for Class 11 Maths Chapter 10 – Straight Lines
Page No 211:
Question 1:
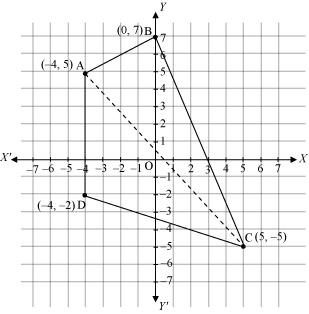
Draw a quadrilateral in the Cartesian plane, whose vertices are (–4, 5), (0, 7), (5, –5) and (–4, –2). Also, find its area.
ANSWER:
Let ABCD be the given quadrilateral with vertices A (–4, 5), B (0, 7), C (5, –5), and D (–4, –2).
Then, by plotting A, B, C, and D on the Cartesian plane and joining AB, BC, CD, and DA, the given quadrilateral can be drawn as
To find the area of quadrilateral ABCD, we draw one diagonal, say AC.
Accordingly, area (ABCD) = area (ΔABC) + area (ΔACD)
We know that the area of a triangle whose vertices are (x1, y1), (x2, y2), and (x3, y3) is
Therefore, area of ΔABC
Area of ΔACD
Thus, area (ABCD)
Page No 211:
Question 2:
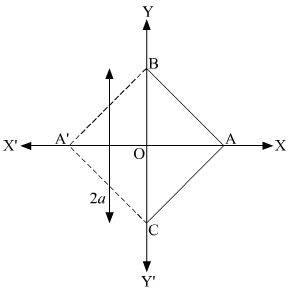
The base of an equilateral triangle with side 2a lies along they y-axis such that the mid point of the base is at the origin. Find vertices of the triangle.
ANSWER:
Let ABC be the given equilateral triangle with side 2a.
Accordingly, AB = BC = CA = 2a
Assume that base BC lies along the y-axis such that the mid-point of BC is at the origin.
i.e., BO = OC = a, where O is the origin.
Now, it is clear that the coordinates of point C are (0, a), while the coordinates of point B are (0, –a).
It is known that the line joining a vertex of an equilateral triangle with the mid-point of its opposite side is perpendicular.
Hence, vertex A lies on the y-axis.
On applying Pythagoras theorem to ΔAOC, we obtain
(AC)2 = (OA)2 + (OC)2
⇒ (2a)2 = (OA)2 + a2
⇒ 4a2 – a2 = (OA)2
⇒ (OA)2 = 3a2
⇒ OA =
∴Coordinates of point A =
Thus, the vertices of the given equilateral triangle are (0, a), (0, –a), and or (0, a), (0, –a), and
.
Page No 211:
Question 3:
Find the distance between and
when: (i) PQ is parallel to the y-axis, (ii) PQ is parallel to the x-axis.
ANSWER:
The given points are and
.
(i) When PQ is parallel to the y-axis, x1 = x2.
In this case, distance between P and Q
(ii) When PQ is parallel to the x-axis, y1 = y2.
In this case, distance between P and Q
Page No 211:
Question 4:
Find a point on the x-axis, which is equidistant from the points (7, 6) and (3, 4).
ANSWER:
Let (a, 0) be the point on the x axis that is equidistant from the points (7, 6) and (3, 4).
On squaring both sides, we obtain
a2 – 14a + 85 = a2 – 6a + 25
⇒ –14a + 6a = 25 – 85
⇒ –8a = –60
Thus, the required point on the x-axis is.
Page No 211:
Question 5:
Find the slope of a line, which passes through the origin, and the mid-point of
the line segment joining the points P (0, –4) and B (8, 0).
ANSWER:
The coordinates of the mid-point of the line segment joining the points
P (0, –4) and B (8, 0) are
It is known that the slope (m) of a non-vertical line passing through the points (x1, y1) and (x2, y2) is given by.
Therefore, the slope of the line passing through (0, 0) and (4, –2) is
.
Hence, the required slope of the line is.
Page No 212:
Question 6:
Without using the Pythagoras theorem, show that the points (4, 4), (3, 5) and (–1, –1) are the vertices of a right angled triangle.
ANSWER:
The vertices of the given triangle are A (4, 4), B (3, 5), and C (–1, –1).
It is known that the slope (m) of a non-vertical line passing through the points (x1, y1) and (x2, y2) is given by.
∴Slope of AB (m1)
Slope of BC (m2)
Slope of CA (m3)
It is observed that m1m3 = –1
This shows that line segments AB and CA are perpendicular to each other
i.e., the given triangle is right-angled at A (4, 4).
Thus, the points (4, 4), (3, 5), and (–1, –1) are the vertices of a right-angled triangle.
Page No 212:
Question 7:
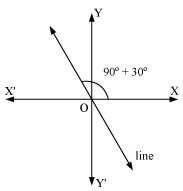
Find the slope of the line, which makes an angle of 30° with the positive direction of y-axis measured anticlockwise.
ANSWER:
If a line makes an angle of 30° with the positive direction of the y-axis measured anticlockwise, then the angle made by the line with the positive direction of the x-axis measured anticlockwise is 90° + 30° = 120°.
Thus, the slope of the given line is tan 120° = tan (180° – 60°) = –tan 60°
Page No 212:
Question 8:
Find the value of x for which the points (x, –1), (2, 1) and (4, 5) are collinear.
ANSWER:
If points A (x, –1), B (2, 1), and C (4, 5) are collinear, then
Slope of AB = Slope of BC
Thus, the required value of x is 1.
Page No 212:
Question 9:
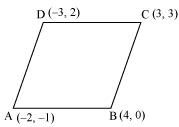
Without using distance formula, show that points (–2, –1), (4, 0), (3, 3) and
(–3, 2) are vertices of a parallelogram.
ANSWER:
Let points (–2, –1), (4, 0), (3, 3), and (–3, 2) be respectively denoted by A, B, C, and D.
Slope of AB
Slope of CD =
⇒ Slope of AB = Slope of CD
⇒ AB and CD are parallel to each other.
Now, slope of BC =
Slope of AD =
⇒ Slope of BC = Slope of AD
⇒ BC and AD are parallel to each other.
Therefore, both pairs of opposite sides of quadrilateral ABCD are parallel. Hence, ABCD is a parallelogram.
Thus, points (–2, –1), (4, 0), (3, 3), and (–3, 2) are the vertices of a parallelogram.
Page No 212:
Question 10:
Find the angle between the x-axis and the line joining the points (3, –1) and (4, –2).
ANSWER:
The slope of the line joining the points (3, –1) and (4, –2) is
Now, the inclination (θ ) of the line joining the points (3, –1) and (4, – 2) is given by
tan θ= –1
⇒ θ = (90° + 45°) = 135°
Thus, the angle between the x-axis and the line joining the points (3, –1) and (4, –2) is 135°.
Page No 212:
Question 11:
The slope of a line is double of the slope of another line. If tangent of the angle between them is, find the slopes of he lines.
ANSWER:
Let be the slopes of the two given lines such that
.
We know that if θisthe angle between the lines l1 and l2 with slopes m1 and m2, then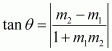
It is given that the tangent of the angle between the two lines is.
Case I
If m = –1, then the slopes of the lines are –1 and –2.
If m =, then the slopes of the lines are
and –1.
Case II
If m = 1, then the slopes of the lines are 1 and 2.
If m =, then the slopes of the lines are
.
Hence, the slopes of the lines are –1 and –2 or and –1 or 1 and 2 or
.
Page No 212:
Question 12:
A line passes through. If slope of the line is m, show that
.
ANSWER:
The slope of the line passing through is
.
It is given that the slope of the line is m.
Hence,
Page No 212:
Question 13:
If three point (h, 0), (a, b) and (0, k) lie on a line, show that.
ANSWER:
If the points A (h, 0), B (a, b), and C (0, k) lie on a line, then
Slope of AB = Slope of BC
On dividing both sides by kh, we obtain
Hence,
Page No 212:
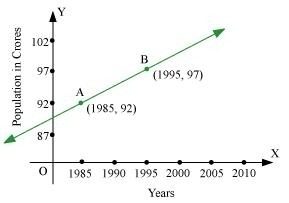
Question 14:
Consider the given population and year graph. Find the slope of the line AB and using it, find what will be the population in the year 2010?
ANSWER:
Since line AB passes through points A (1985, 92) and B (1995, 97), its slope is
Let y be the population in the year 2010. Then, according to the given graph, line AB must pass through point C (2010, y).
∴Slope of AB = Slope of BC
Thus, the slope of line AB is, while in the year 2010, the population will be 104.5 crores.
Page No 219:
Question 1:
Write the equations for the x and y-axes.
ANSWER:
The y-coordinate of every point on the x-axis is 0.
Therefore, the equation of the x-axis is y = 0.
The x-coordinate of every point on the y-axis is 0.
Therefore, the equation of the y-axis is x = 0.
Page No 219:
Question 2:
Find the equation of the line which passes through the point (–4, 3) with slope.
ANSWER:
We know that the equation of the line passing through point, whose slope is m, is
.
Thus, the equation of the line passing through point (–4, 3), whose slope is, is
Page No 219:
Question 3:
Find the equation of the line which passes though (0, 0) with slope m.
ANSWER:
We know that the equation of the line passing through point, whose slope is m, is
.
Thus, the equation of the line passing through point (0, 0), whose slope is m,is
(y – 0) = m(x – 0)
i.e., y = mx
Page No 219:
Question 4:
Find the equation of the line which passes though and is inclined with the x-axis at an angle of 75°.
ANSWER:
The slope of the line that inclines with the x-axis at an angle of 75° is
m = tan 75°
We know that the equation of the line passing through point, whose slope is m, is
.
Thus, if a line passes thoughand inclines with the x-axis at an angle of 75°, then the equation of the line is given as
Page No 219:
Question 5:
Find the equation of the line which intersects the x-axis at a distance of 3 units to the left of origin with slope –2.
ANSWER:
It is known that if a line with slope m makes x-intercept d, then the equation of the line is given as
y = m(x – d)
For the line intersecting the x-axis at a distance of 3 units to the left of the origin, d = –3.
The slope of the line is given as m = –2
Thus, the required equation of the given line is
y = –2 [x – (–3)]
y = –2x – 6
i.e., 2x + y + 6 = 0
Page No 219:
Question 6:
Find the equation of the line which intersects the y-axis at a distance of 2 units above the origin and makes an angle of 30° with the positive direction of the x-axis.
ANSWER:
It is known that if a line with slope m makes y-intercept c, then the equation of the line is given as
y = mx + c
Here, c = 2 and m = tan 30°.
Thus, the required equation of the given line is
Page No 219:
Question 7:
Find the equation of the line which passes through the points (–1, 1) and (2, –4).
ANSWER:
It is known that the equation of the line passing through points (x1, y1) and (x2, y2) is.
Therefore, the equation of the line passing through the points (–1, 1) and
(2, –4) is
Page No 220:
Question 8:
Find the equation of the line which is at a perpendicular distance of 5 units from the origin and the angle made by the perpendicular with the positive x-axis is 30°
ANSWER:
If p is the length of the normal from the origin to a line and ω is the angle made by the normal with the positive direction of the x-axis, then the equation of the line is given by xcos ω + y sin ω = p.
Here, p = 5 units and ω = 30°
Thus, the required equation of the given line is
x cos 30° + y sin 30° = 5
Page No 220:
Question 9:
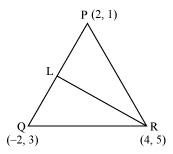
The vertices of ΔPQR are P (2, 1), Q (–2, 3) and R (4, 5). Find equation of the median through the vertex R.
ANSWER:
It is given that the vertices of ΔPQR are P (2, 1), Q (–2, 3), and R (4, 5).
Let RL be the median through vertex R.
Accordingly, L is the mid-point of PQ.
By mid-point formula, the coordinates of point L are given by
It is known that the equation of the line passing through points (x1, y1) and (x2, y2) is.
Therefore, the equation of RL can be determined by substituting (x1, y1) = (4, 5) and (x2, y2) = (0, 2).
Hence,
Thus, the required equation of the median through vertex R is.
Page No 220:
Question 10:
Find the equation of the line passing through (–3, 5) and perpendicular to the line through the points (2, 5) and (–3, 6).
ANSWER:
The slope of the line joining the points (2, 5) and (–3, 6) is
We know that two non-vertical lines are perpendicular to each other if and only if their slopes are negative reciprocals of each other.
Therefore, slope of the line perpendicular to the line through the points (2, 5) and (–3, 6)
Now, the equation of the line passing through point (–3, 5), whose slope is 5, is
Page No 220:
Question 11:
A line perpendicular to the line segment joining the points (1, 0) and (2, 3) divides it in the ratio 1:n. Find the equation of the line.
ANSWER:
According to the section formula, the coordinates of the point that divides the line segment joining the points (1, 0) and (2, 3) in the ratio 1: n is given by
The slope of the line joining the points (1, 0) and (2, 3) is
We know that two non-vertical lines are perpendicular to each other if and only if their slopes are negative reciprocals of each other.
Therefore, slope of the line that is perpendicular to the line joining the points (1, 0) and (2, 3)
Now, the equation of the line passing through and whose slope is
is given by
Page No 220:
Question 12:
Find the equation of a line that cuts off equal intercepts on the coordinate axes and passes through the point (2, 3).
ANSWER:
The equation of a line in the intercept form is
Here, a and b are the intercepts on x and y axes respectively.
It is given that the line cuts off equal intercepts on both the axes. This means that a = b.
Accordingly, equation (i) reduces to
Since the given line passes through point (2, 3), equation (ii) reduces to
2 + 3 = a ⇒ a = 5
On substituting the value of a in equation (ii), we obtain
x + y = 5, which is the required equation of the line
Page No 220:
Question 13:
Find equation of the line passing through the point (2, 2) and cutting off intercepts on the axes whose sum is 9.
ANSWER:
The equation of a line in the intercept form is
Here, a and b are the intercepts on x and y axes respectively.
It is given thata + b = 9 ⇒ b = 9 – a … (ii)
From equations (i) and (ii), we obtain
It is given that the line passes through point (2, 2). Therefore, equation (iii) reduces to
If a = 6 and b = 9 – 6 = 3, then the equation of the line is
If a = 3 and b = 9 – 3 = 6, then the equation of the line is
Page No 220:
Question 14:
Find equation of the line through the point (0, 2) making an angle with the positive x-axis. Also, find the equation of line parallel to it and crossing the y-axis at a distance of 2 units below the origin.
ANSWER:
The slope of the line making an anglewith the positive x-axis is
Now, the equation of the line passing through point (0, 2) and having a slope is
.
The slope of line parallel to line is
.
It is given that the line parallel to linecrosses the y-axis 2 units below the origin i.e., it passes through point (0, –2).
Hence, the equation of the line passing through point (0, –2) and having a slope is
Page No 220:
Question 15:
The perpendicular from the origin to a line meets it at the point (– 2, 9), find the equation of the line.
ANSWER:
The slope of the line joining the origin (0, 0) and point (–2, 9) is
Accordingly, the slope of the line perpendicular to the line joining the origin and point (– 2, 9) is
Now, the equation of the line passing through point (–2, 9) and having a slope m2 is
Page No 220:
Question 16:
The length L (in centimetre) of a copper rod is a linear function of its Celsius temperature C. In an experiment, if L = 124.942 when C = 20 and L = 125.134 when C = 110, express L in terms of C.
ANSWER:
It is given that when C = 20, the value of L is 124.942, whereas when C = 110, the value of L is 125.134.
Accordingly, points (20, 124.942) and (110, 125.134) satisfy the linear relation between L and C.
Now, assuming C along the x-axis and L along the y-axis, we have two points i.e., (20, 124.942) and (110, 125.134) in the XY plane.
Therefore, the linear relation between L and C is the equation of the line passing through points (20, 124.942) and (110, 125.134).
(L – 124.942) =
Page No 220:
Question 17:
The owner of a milk store finds that, he can sell 980 litres of milk each week at Rs 14/litre and 1220 litres of milk each week at Rs 16/litre. Assuming a linear relationship between selling price and demand, how many litres could he sell weekly at Rs 17/litre?
ANSWER:
The relationship between selling price and demand is linear.
Assuming selling price per litre along the x-axis and demand along the y-axis, we have two points i.e., (14, 980) and (16, 1220) in the XY plane that satisfy the linear relationship between selling price and demand.
Therefore, the linear relationship between selling price per litre and demand is the equation of the line passing through points (14, 980) and (16, 1220).
When x = Rs 17/litre,
Thus, the owner of the milk store could sell 1340 litres of milk weekly at Rs 17/litre.
Page No 220:
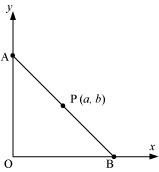
Question 18:
P (a, b) is the mid-point of a line segment between axes. Show that equation of the line is
ANSWER:
Let AB be the line segment between the axes and let P (a, b) be its mid-point.
Let the coordinates of A and B be (0, y) and (x, 0) respectively.
Since P (a, b) is the mid-point of AB,
Thus, the respective coordinates of A and B are (0, 2b) and (2a, 0).
The equation of the line passing through points (0, 2b) and (2a, 0) is
On dividing both sides by ab, we obtain
Thus,the equation of the line is.
Page No 220:
Question 19:
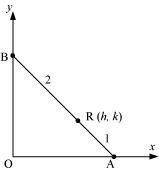
Point R (h, k) divides a line segment between the axes in the ratio 1:2. Find equation of the line.
ANSWER:
Let AB be the line segment between the axes such that point R (h, k) divides AB in the ratio 1: 2.
Let the respective coordinates of A and B be (x, 0) and (0, y).
Since point R (h, k) divides AB in the ratio 1: 2, according to the section formula,
Therefore, the respective coordinates of A and B are and (0, 3k).
Now, the equation of line AB passing through points and
(0, 3k) is
Thus,the required equation of the line is 2kx + hy = 3hk.
Page No 220:
Question 20:
By using the concept of equation of a line, prove that the three points (3, 0),
(–2, –2) and (8, 2) are collinear.
ANSWER:
In order to show that points (3, 0), (–2, –2), and (8, 2) are collinear, it suffices to show that the line passing through points (3, 0) and (–2, –2) also passes through point (8, 2).
The equation of the line passing through points (3, 0) and (–2, –2) is
It is observed that at x = 8 and y = 2,
L.H.S. = 2 × 8 – 5 × 2 = 16 – 10 = 6 = R.H.S.
Therefore, the line passing through points (3, 0) and (–2, –2) also passes through point (8, 2). Hence, points (3, 0), (–2, –2), and (8, 2) are collinear.
Page No 227:
Question 1:
Reduce the following equations into slope-intercept form and find their slopes and the y-intercepts.
(i) x + 7y = 0 (ii) 6x + 3y – 5 = 0 (iii) y = 0
ANSWER:
(i) The given equation is x + 7y = 0.
It can be written as
This equation is of the form y = mx + c, where.
Therefore, equation (1) is in the slope-intercept form, where the slope and the y-intercept are and 0 respectively.
(ii) The given equation is 6x + 3y – 5 = 0.
It can be written as
Therefore, equation (2) is in the slope-intercept form, where the slope and the y-intercept are–2 and respectively.
(iii) The given equation is y = 0.
It can be written as
y = 0.x + 0 … (3)
This equation is of the form y = mx + c, where m = 0 and c = 0.
Therefore, equation (3) is in the slope-intercept form, where the slope and the y-intercept are 0 and 0 respectively.
Page No 227:
Question 2:
Reduce the following equations into intercept form and find their intercepts on the axes.
(i) 3x + 2y – 12 = 0 (ii) 4x – 3y = 6 (iii) 3y + 2 = 0.
ANSWER:
(i) The given equation is 3x + 2y – 12 = 0.
It can be written as
This equation is of the form, where a = 4 and b = 6.
Therefore, equation (1) is in the intercept form, where the intercepts on the x and y axes are 4 and 6 respectively.
(ii) The given equation is 4x – 3y = 6.
It can be written as
This equation is of the form, where a =
and b = –2.
Therefore, equation (2) is in the intercept form, where the intercepts on the x and y axes are and –2 respectively.
(iii) The given equation is 3y + 2 = 0.
It can be written as
This equation is of the form, where a = 0 and b =
.
Therefore, equation (3) is in the intercept form, where the intercept on the y-axis is and it has no intercept on the x-axis.
Page No 227:
Question 3:
Reduce the following equations into normal form. Find their perpendicular distances from the origin and angle between perpendicular and the positive x-axis.
(i) (ii) y – 2 = 0 (iii) x – y = 4
ANSWER:
(i) The given equation is.
It can be reduced as:
On dividing both sides by, we obtain
Equation (1) is in the normal form.
On comparing equation (1) with the normal form of equation of line
x cos ω + y sin ω = p, we obtain ω = 120° and p = 4.
Thus, the perpendicular distance of the line from the origin is 4, while the angle between the perpendicular and the positive x-axis is 120°.
(ii) The given equation is y – 2 = 0.
It can be reduced as 0.x + 1.y = 2
On dividing both sides by, we obtain 0.x + 1.y = 2
⇒ x cos 90° + y sin 90° = 2 … (1)
Equation (1) is in the normal form.
On comparing equation (1) with the normal form of equation of line
x cos ω + y sin ω = p, we obtain ω = 90° and p = 2.
Thus, the perpendicular distance of the line from the origin is 2, while the angle between the perpendicular and the positive x-axis is 90°.
(iii) The given equation is x – y = 4.
It can be reduced as 1.x + (–1) y = 4
On dividing both sides by, we obtain
Equation (1) is in the normal form.
On comparing equation (1) with the normal form of equation of line
x cos ω + y sin ω = p, we obtain ω = 315° and .
Thus, the perpendicular distance of the line from the origin is, while the angle between the perpendicular and the positive x-axis is 315°.
Page No 227:
Question 4:
Find the distance of the point (–1, 1) from the line 12(x + 6) = 5(y – 2).
ANSWER:
The given equation of the line is 12(x + 6) = 5(y – 2).
⇒ 12x + 72 = 5y – 10
⇒12x – 5y + 82 = 0 … (1)
On comparing equation (1) with general equation of line Ax + By + C = 0, we obtain A = 12, B = –5, and C = 82.
It is known that the perpendicular distance (d) of a line Ax + By + C = 0 from a point (x1, y1) is given by.
The given point is (x1, y1) = (–1, 1).
Therefore, the distance of point (–1, 1) from the given line
Page No 227:
Question 5:
Find the points on the x-axis, whose distances from the line are 4 units.
ANSWER:
The given equation of line is
On comparing equation (1) with general equation of line Ax + By + C = 0, we obtain A = 4, B = 3, and C = –12.
Let (a, 0) be the point on the x-axis whose distance from the given line is 4 units.
It is known that the perpendicular distance (d) of a line Ax + By + C = 0 from a point (x1, y1) is given by.
Therefore,
Thus, the required points on the x-axis are (–2, 0) and (8, 0).
Page No 227:
Question 6:
Find the distance between parallel lines
(i) 15x + 8y – 34 = 0 and 15x + 8y + 31 = 0
(ii) l (x + y) + p = 0 and l (x + y) – r = 0
ANSWER:
It is known that the distance (d) between parallel lines Ax + By + C1 = 0 and Ax + By + C2 = 0 is given by.
(i) The given parallel lines are 15x + 8y – 34 = 0 and 15x + 8y + 31 = 0.
Here, A = 15, B = 8, C1 = –34, and C2 = 31.
Therefore, the distance between the parallel lines is
(ii) The given parallel lines are l (x + y) + p = 0 and l (x + y) – r = 0.
lx + ly + p = 0 and lx + ly – r = 0
Here, A = l, B = l, C1 = p, and C2 = –r.
Therefore, the distance between the parallel lines is
Page No 228:
Question 7:
Find equation of the line parallel to the line 3x – 4y + 2 = 0 and passing through the point (–2, 3).
ANSWER:
The equation of the given line is
, which is of the form y = mx + c
∴ Slope of the given line
It is known that parallel lines have the same slope.
∴ Slope of the other line =
Now, the equation of the line that has a slope of and passes through the point (–2, 3) is
Page No 228:
Question 8:
Find equation of the line perpendicular to the line x – 7y + 5 = 0 and having x intercept 3.
ANSWER:
The given equation of line is.
, which is of the form y = mx + c
∴Slope of the given line
The slope of the line perpendicular to the line having a slope of is
The equation of the line with slope –7 and x-intercept 3 is given by
y = m (x – d)
⇒ y = –7 (x – 3)
⇒ y = –7x + 21
⇒ 7x + y = 21
Page No 228:
Question 9:
Find angles between the lines
ANSWER:
The given lines are.
The slope of line (1) is, while the slope of line (2) is
.
The acute angle i.e., θ between the two lines is given by
Thus, the angle between the given lines is either 30° or 180° – 30° = 150°.
Page No 228:
Question 10:
The line through the points (h, 3) and (4, 1) intersects the line 7x – 9y – 19 = 0. at right angle. Find the value of h.
ANSWER:
The slope of the line passing through points (h, 3) and (4, 1) is
The slope of line 7x – 9y – 19 = 0 or is
.
It is given that the two lines are perpendicular.
Thus, the value of h is.
Page No 228:
Question 11:
Prove that the line through the point (x1, y1) and parallel to the line Ax + By + C = 0 is A (x –x1) + B (y – y1) = 0.
ANSWER:
The slope of line Ax + By + C = 0 or is
It is known that parallel lines have the same slope.
∴ Slope of the other line =
The equation of the line passing through point (x1, y1) and having a slope is
Hence, the line through point (x1, y1) and parallel to line Ax + By + C = 0 is
A (x –x1) + B (y – y1) = 0
Page No 228:
Question 12:
Two lines passing through the point (2, 3) intersects each other at an angle of 60°. If slope of one line is 2, find equation of the other line.
ANSWER:
It is given that the slope of the first line, m1 = 2.
Let the slope of the other line be m2.
The angle between the two lines is 60°.
The equation of the line passing through point (2, 3) and having a slope of 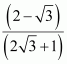
In this case, the equation of the other line is.
The equation of the line passing through point (2, 3) and having a slope of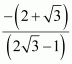
In this case, the equation of the other line is.
Thus, the required equation of the other line is or
.
Page No 228:
Question 13:
Find the equation of the right bisector of the line segment joining the points (3, 4) and (–1, 2).
ANSWER:
The right bisector of a line segment bisects the line segment at 90°.
The end-points of the line segment are given as A (3, 4) and B (–1, 2).
Accordingly, mid-point of AB
Slope of AB
∴Slope of the line perpendicular to AB =
The equation of the line passing through (1, 3) and having a slope of –2 is
(y – 3) = –2 (x – 1)
y – 3 = –2x + 2
2x + y = 5
Thus, the required equation of the line is 2x + y = 5.
Page No 228:
Question 14:
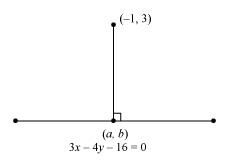
Find the coordinates of the foot of perpendicular from the point (–1, 3) to the line 3x – 4y – 16 = 0.
ANSWER:
Let (a, b) be the coordinates of the foot of the perpendicular from the point (–1, 3) to the line 3x – 4y – 16 = 0.
Slope of the line joining (–1, 3) and (a, b), m1
Slope of the line 3x – 4y – 16 = 0 or
Since these two lines are perpendicular, m1m2 = –1
Point (a, b) lies on line 3x – 4y = 16.
∴3a – 4b = 16 … (2)
On solving equations (1) and (2), we obtain
Thus, the required coordinates of the foot of the perpendicular are.
Page No 228:
Question 15:
The perpendicular from the origin to the line y = mx + c meets it at the point
(–1, 2). Find the values of m and c.
ANSWER:
The given equation of line is y = mx + c.
It is given that the perpendicular from the origin meets the given line at (–1, 2).
Therefore, the line joining the points (0, 0) and (–1, 2) is perpendicular to the given line.
∴Slope of the line joining (0, 0) and (–1, 2)
The slope of the given line is m.
Since point (–1, 2) lies on the given line, it satisfies the equation y = mx + c.
Thus, the respective values of m and c are.
Page No 228:
Question 16:
If p and q are the lengths of perpendiculars from the origin to the lines x cos θ – y sin θ = k cos 2θ and x sec θ+ y cosec θ = k, respectively, prove that p2 + 4q2 = k2
ANSWER:
The equations of given lines are
x cos θ – y sinθ = k cos 2θ … (1)
x secθ + y cosec θ= k … (2)
The perpendicular distance (d) of a line Ax + By + C = 0 from a point (x1, y1) is given by.
On comparing equation (1) to the general equation of line i.e., Ax + By + C = 0, we obtain A = cosθ, B = –sinθ, and C = –k cos 2θ.
It is given that p is the length of the perpendicular from (0, 0) to line (1).
On comparing equation (2) to the general equation of line i.e., Ax + By + C = 0, we obtain A = secθ, B = cosecθ, and C = –k.
It is given that q is the length of the perpendicular from (0, 0) to line (2).
From (3) and (4), we have
Hence, we proved that p2 + 4q2 = k2.
Page No 228:
Question 17:
In the triangle ABC with vertices A (2, 3), B (4, –1) and C (1, 2), find the equation and length of altitude from the vertex A.
ANSWER:
Let AD be the altitude of triangle ABC from vertex A.
Accordingly, AD⊥BC
The equation of the line passing through point (2, 3) and having a slope of 1 is
(y – 3) = 1(x – 2)
⇒ x – y + 1 = 0
⇒ y – x = 1
Therefore, equation of the altitude from vertex A = y – x = 1.
Length of AD = Length of the perpendicular from A (2, 3) to BC
The equation of BC is
The perpendicular distance (d) of a line Ax + By + C = 0 from a point (x1, y1) is given by.
On comparing equation (1) to the general equation of line Ax + By + C = 0, we obtain A = 1, B = 1, and C = –3.
∴Length of AD
Thus, the equation and the length of the altitude from vertex A are y – x = 1 and units respectively.
Page No 228:
Question 18:
If p is the length of perpendicular from the origin to the line whose intercepts on the axes are a and b, then show that.
ANSWER:
It is known that the equation of a line whose intercepts on the axes are a and b is
The perpendicular distance (d) of a line Ax + By + C = 0 from a point (x1, y1) is given by.
On comparing equation (1) to the general equation of line Ax + By + C = 0, we obtain A = b, B = a, and C = –ab.
Therefore, if p is the length of the perpendicular from point (x1, y1) = (0, 0) to line (1), we obtain
On squaring both sides, we obtain
Hence, we showed that.
Page No 233:
Question 1:
Find the values of k for which the lineis
(a) Parallel to the x-axis,
(b) Parallel to the y-axis,
(c) Passing through the origin.
ANSWER:
The given equation of line is
(k – 3) x – (4 – k2) y + k2 – 7k + 6 = 0 … (1)
(a) If the given line is parallel to the x-axis, then
Slope of the given line = Slope of the x-axis
The given line can be written as
(4 – k2) y = (k – 3) x + k2 – 7k + 6 = 0
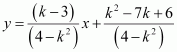
∴Slope of the given line =
Slope of the x-axis = 0
Thus, if the given line is parallel to the x-axis, then the value of k is 3.
(b) If the given line is parallel to the y-axis, it is vertical. Hence, its slope will be undefined.
The slope of the given line is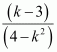
Now, 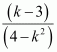
k2 = 4
⇒ k = ±2
Thus, if the given line is parallel to the y-axis, then the value of k is ±2.
(c) If the given line is passing through the origin, then point (0, 0) satisfies the
given equation of line.
Thus, if the given line is passing through the origin, then the value of k is either 1 or 6.
Page No 233:
Question 2:
Find the values of θand p, if the equation is the normal form of the line
.
ANSWER:
The equation of the given line is.
This equation can be reduced as
On dividing both sides by, we obtain
On comparing equation (1) to, we obtain
Since the values of sin θ and cos θ are negative,
Thus, the respective values of θand p are and 1
Page No 233:
Question 3:
Find the equations of the lines, which cut-off intercepts on the axes whose sum and product are 1 and –6, respectively.
ANSWER:
Let the intercepts cut by the given lines on the axes be a and b.
It is given that
a + b = 1 … (1)
ab = –6 … (2)
On solving equations (1) and (2), we obtain
a = 3 and b = –2 or a = –2 and b = 3
It is known that the equation of the line whose intercepts on the axes are a and b is
Case I: a = 3 and b = –2
In this case, the equation of the line is –2x + 3y + 6 = 0, i.e., 2x – 3y = 6.
Case II: a = –2 and b = 3
In this case, the equation of the line is 3x – 2y + 6 = 0, i.e., –3x + 2y = 6.
Thus, the required equation of the lines are 2x – 3y = 6 and –3x + 2y = 6.
Page No 233:
Question 4:
What are the points on the y-axis whose distance from the line is 4 units.
ANSWER:
Let (0, b) be the point on the y-axis whose distance from line is 4 units.
The given line can be written as 4x + 3y – 12 = 0 … (1)
On comparing equation (1) to the general equation of line Ax + By + C = 0, we obtain A = 4, B = 3, and C = –12.
It is known that the perpendicular distance (d) of a line Ax + By + C = 0 from a point (x1, y1) is given by.
Therefore, if (0, b) is the point on the y-axis whose distance from line is 4 units, then:
Thus, the required points are and
.
Page No 233:
Question 5:
Find the perpendicular distance from the origin to the line joining the points
ANSWER:
The equation of the line joining the points is given by
It is known that the perpendicular distance (d) of a line Ax + By + C = 0 from a point (x1, y1) is given by.
Therefore, the perpendicular distance (d) of the given line from point (x1, y1) = (0, 0) is
Page No 233:
Question 6:
Find the equation of the line parallel to y-axis and drawn through the point of intersection of the lines x – 7y + 5 = 0 and 3x + y = 0.
ANSWER:
The equation of any line parallel to the y-axis is of the form
x = a … (1)
The two given lines are
x – 7y + 5 = 0 … (2)
3x + y = 0 … (3)
On solving equations (2) and (3), we obtain.
Therefore, is the point of intersection of lines (2) and (3).
Since line x = a passes through point,
.
Thus, the required equation of the line is.
Page No 233:
Question 7:
Find the equation of a line drawn perpendicular to the line through the point, where it meets the y-axis.
ANSWER:
The equation of the given line is.
This equation can also be written as 3x + 2y – 12 = 0
, which is of the form y = mx + c
∴Slope of the given line
∴Slope of line perpendicular to the given line
Let the given line intersect the y-axis at (0, y).
On substituting x with 0 in the equation of the given line, we obtain
∴The given line intersects the y-axis at (0, 6).
The equation of the line that has a slope of and passes through point (0, 6) is
Thus, the required equation of the line is.
Page No 233:
Question 8:
Find the area of the triangle formed by the lines y – x = 0, x + y = 0 and x – k = 0.
ANSWER:
The equations of the given lines are
y – x = 0 … (1)
x + y = 0 … (2)
x – k = 0 … (3)
The point of intersection of lines (1) and (2) is given by
x = 0 and y = 0
The point of intersection of lines (2) and (3) is given by
x = k and y = –k
The point of intersection of lines (3) and (1) is given by
x = k and y = k
Thus, the vertices of the triangle formed by the three given lines are (0, 0), (k, –k), and (k, k).
We know that the area of a triangle whose vertices are (x1, y1), (x2, y2), and (x3, y3) is.
Therefore, area of the triangle formed by the three given lines
Page No 233:
Question 9:
Find the value of p so that the three lines 3x + y – 2 = 0, px + 2y – 3 = 0 and 2x – y – 3 = 0 may intersect at one point.
ANSWER:
The equations of the given lines are
3x + y – 2 = 0 … (1)
px + 2y – 3 = 0 … (2)
2x – y – 3 = 0 … (3)
On solving equations (1) and (3), we obtain
x = 1 and y = –1
Since these three lines may intersect at one point, the point of intersection of lines (1) and (3) will also satisfy line (2).
p (1) + 2 (–1) – 3 = 0
p – 2 – 3 = 0
p = 5
Thus, the required value of p is 5.
Page No 233:
Question 10:
If three lines whose equations are
concurrent, then show that
ANSWER:
The equations of the given lines are
y = m1x + c1 … (1)
y = m2x + c2 … (2)
y = m3x + c3 … (3)
On subtracting equation (1) from (2), we obtain
On substituting this value of x in (1), we obtain
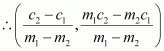
It is given that lines (1), (2), and (3) are concurrent. Hence, the point of intersection of lines (1) and (2) will also satisfy equation (3).
Hence,
Page No 233:
Question 11:
Find the equation of the lines through the point (3, 2) which make an angle of 45° with the line x –2y = 3.
ANSWER:
Let the slope of the required line be m1.
The given line can be written as , which is of the form y = mx + c
∴Slope of the given line =
It is given that the angle between the required line and line x – 2y = 3 is 45°.
We know that if θisthe acute angle between lines l1 and l2 with slopes m1 and m2 respectively, then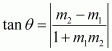
Case I: m1 = 3
The equation of the line passing through (3, 2) and having a slope of 3 is:
y – 2 = 3 (x – 3)
y – 2 = 3x – 9
3x – y = 7
Case II: m1 =
The equation of the line passing through (3, 2) and having a slope of is:
Thus, the equations of the lines are 3x – y = 7 and x + 3y = 9.
Page No 233:
Question 12:
Find the equation of the line passing through the point of intersection of the lines 4x + 7y – 3 = 0 and 2x – 3y + 1 = 0 that has equal intercepts on the axes.
ANSWER:
Let the equation of the line having equal intercepts on the axes be
On solving equations 4x + 7y – 3 = 0 and 2x – 3y + 1 = 0, we obtain.
is the point of intersection of the two given lines.
Since equation (1) passes through point,
∴ Equation (1) becomes
Thus, the required equation of the line is.
Page No 234:
Question 13:
Show that the equation of the line passing through the origin and making an angle θwith the line.
ANSWER:
Let the equation of the line passing through the origin be y = m1x.
If this line makes an angle of θ with line y = mx + c, then angle θ is given by
Case I:
Case II:
Therefore, the required line is given by.
Page No 234:
Question 14:
In what ratio, the line joining (–1, 1) and (5, 7) is divided by the line
x + y = 4?
ANSWER:
The equation of the line joining the points (–1, 1) and (5, 7) is given by
The equation of the given line is
x + y – 4 = 0 … (2)
The point of intersection of lines (1) and (2) is given by
x = 1 and y = 3
Let point (1, 3) divide the line segment joining (–1, 1) and (5, 7) in the ratio 1:k. Accordingly, by section formula,
Thus, the line joining the points (–1, 1) and (5, 7) is divided by line
x + y = 4 in the ratio 1:2.
Page No 234:
Question 15:
Find the distance of the line 4x + 7y + 5 = 0 from the point (1, 2) along the line 2x – y = 0.
ANSWER:
The given lines are
2x – y = 0 … (1)
4x + 7y + 5 = 0 … (2)
A (1, 2) is a point on line (1).
Let B be the point of intersection of lines (1) and (2).
On solving equations (1) and (2), we obtain.
∴Coordinates of point B are.
By using distance formula, the distance between points A and B can be obtained as
Thus, the required distance is.
Page No 234:
Question 16:
Find the direction in which a straight line must be drawn through the point (–1, 2) so that its point of intersection with the line x + y = 4 may be at a distance of 3 units from this point.
ANSWER:
Let y = mx + c be the line through point (–1, 2).
Accordingly, 2 = m (–1) + c.
⇒ 2 = –m + c
⇒ c = m + 2
∴ y = mx + m + 2 … (1)
The given line is
x + y = 4 … (2)
On solving equations (1) and (2), we obtain
is the point of intersection of lines (1) and (2).
Since this point is at a distance of 3 units from point (– 1, 2), according to distance formula,
Thus, the slope of the required line must be zero i.e., the line must be parallel to the x-axis.
Page No 234:
Question 17:
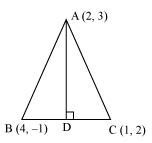
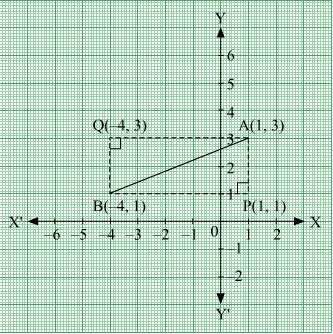
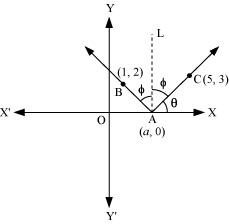
The hypotenuse of a right angled triangle has its ends at the points (1, 3) and (−4, 1). Find the equation of the legs (perpendicular sides) of the triangle.
ANSWER:
Let A(1,3) and B(−4,1) be the coordinates of the end points of the hypotenuse.
Now, plotting the line segment joining the points A(1,3) and B(−4,1) on the coordinate plane, we will get two right triangles with AB as the hypotenuse. Now from the diagram, it is clear that the point of intersection of the other two legs of the right triangle having AB as the hypotenuse can be either P or Q.
CASE 1: When ∆ APB is taken.
The perpendicular sides in ∆ APB are AP and PB.
Now, side PB is parallel to x-axis and at a distance of 1 units above x-axis.
So, equation of PB is, y=1 or y−1=0.
The side AP is parallel to y-axis and at a distance of 1 units on the right of y-axis.
So, equation of AP is x=1 or x−1=0.
CASE 2: When ∆ AQB is taken.
The perpendicular sides in ∆ AQB are AQ and QB.
Now, side AQ is parallel to x-axis and at a distance of 3 units above x-axis.
So, equation of AQ is, y=3 or y−3=0.
The side QB is parallel to y-axis and at a distance of 4 units on the left of y-axis.
So, equation of QB is x=−4 or x+4=0.
Hence, the equation of the legs are :
x=1, y=1 or x=−4, y=3
Page No 234:
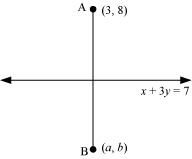
Question 18:
Find the image of the point (3, 8) with respect to the line x + 3y = 7 assuming the line to be a plane mirror.
ANSWER:
The equation of the given line is
x + 3y = 7 … (1)
Let point B (a, b) be the image of point A (3, 8).
Accordingly, line (1) is the perpendicular bisector of AB.
Since line (1) is perpendicular to AB,
The mid-point of line segment AB will also satisfy line (1).
Hence, from equation (1), we have
On solving equations (2) and (3), we obtain a = –1 and b = –4.
Thus, the image of the given point with respect to the given line is (–1, –4).
Page No 234:
Question 19:
If the lines y = 3x + 1 and 2y = x + 3 are equally inclined to the line y = mx + 4, find the value of m.
ANSWER:
The equations of the given lines are
y = 3x + 1 … (1)
2y = x + 3 … (2)
y = mx + 4 … (3)
Slope of line (1), m1 = 3
Slope of line (2),
Slope of line (3), m3 = m
It is given that lines (1) and (2) are equally inclined to line (3). This means that
the angle between lines (1) and (3) equals the angle between lines (2) and (3).
Thus, the required value of m is.
Page No 234:
Question 20:
If sum of the perpendicular distances of a variable point P (x, y) from the lines x + y – 5 = 0 and 3x – 2y + 7 = 0 is always 10. Show that P must move on a line.
ANSWER:
The equations of the given lines are
x + y – 5 = 0 … (1)
3x – 2y + 7 = 0 … (2)
The perpendicular distances of P (x, y) from lines (1) and (2) are respectively given by
It is given that.
, which is the equation of a line.
Similarly, we can obtain the equation of line for any signs of.
Thus, point P must move on a line.
Page No 234:
Question 21:
Find equation of the line which is equidistant from parallel lines 9x + 6y – 7 = 0 and 3x + 2y + 6 = 0.
ANSWER:
The equations of the given lines are
9x + 6y – 7 = 0 … (1)
3x + 2y + 6 = 0 … (2)
Let P (h, k) be the arbitrary point that is equidistant from lines (1) and (2). The perpendicular distance of P (h, k) from line (1) is given by
The perpendicular distance of P (h, k) from line (2) is given by
Since P (h, k) is equidistant from lines (1) and (2),
∴
9h + 6k – 7 = – 9h – 6k – 18
⇒ 18h + 12k + 11 = 0
Thus, the required equation of the line is 18x + 12y + 11 = 0.
Page No 234:
Question 22:
A ray of light passing through the point (1, 2) reflects on the x-axis at point A and the reflected ray passes through the point (5, 3). Find the coordinates of A.
ANSWER:
Let the coordinates of point A be (a, 0).
Draw a line (AL) perpendicular to the x-axis.
We know that angle of incidence is equal to angle of reflection. Hence, let
∠BAL = ∠CAL = Φ
Let ∠CAX = θ
∴∠OAB = 180° – (θ + 2Φ) = 180° – [θ + 2(90° – θ)]
= 180° – θ – 180° + 2θ
= θ
∴∠BAX = 180° – θ
From equations (1) and (2), we obtain
Thus, the coordinates of point A are.
Page No 234:
Question 23:
Prove that the product of the lengths of the perpendiculars drawn from the points
ANSWER:
The equation of the given line is
Length of the perpendicular from point to line (1) is
Length of the perpendicular from point to line (2) is
On multiplying equations (2) and (3), we obtain
Hence, proved.
Page No 234:
Question 24:
A person standing at the junction (crossing) of two straight paths represented by the equations 2x – 3y + 4 = 0 and 3x + 4y – 5 = 0 wants to reach the path whose equation is 6x – 7y + 8 = 0 in the least time. Find equation of the path that he should follow.
ANSWER:
The equations of the given lines are
2x – 3y + 4 = 0 … (1)
3x + 4y – 5 = 0 … (2)
6x – 7y + 8 = 0 … (3)
The person is standing at the junction of the paths represented by lines (1) and (2).
On solving equations (1) and (2), we obtain.
Thus, the person is standing at point.
The person can reach path (3) in the least time if he walks along the perpendicular line to (3) from point.
∴Slope of the line perpendicular to line (3)
The equation of the line passing through and having a slope of
is given by
Hence, the path that the person should follow is.